This is an exercise for code newbies. It actually doesn't require any programming, just a little bit of calculation:
Consider a service such as bit.ly that generate short Urls
Assume that the generated key is always 7 alphanumeric characters long (using both upper case and lower case letters)
Suppose people around the world are generating short Urls at a rate of 1000 short Urls every second.
Question: How long takes until bit.ly runs out of unique sequences for the short Urls?

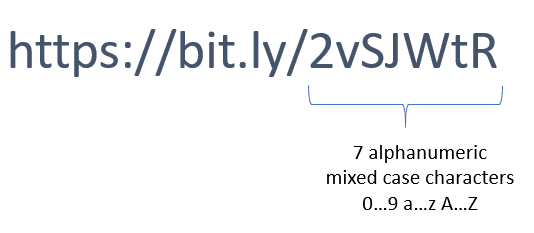





Top comments (3)
So first we have to calculate the number of possible URLs.
Each character can has 62 possible outcomes (26 + 26 +10).
And we have 7 alphanumeric characters.
Since the order of the characters is important (/abcde != /edcba) we have to apply the permutation 👨🎓.
But since we are replacing characters we have chosen before (e.g. /aaaa is possible) we have to use permutations with replacements.
So now that we have the number of possible URLs we just have to divide it by the frequency of the URLs being created.
So bit.ly would run out in about 56,800,235 seconds (about 658 days).
why 62 ^ 6?
Should have read the task better. It's 7 digits so it should have been 62^7