In the previous article we saw how to approximate π by calculating the area of a circle using JavaScript.
In this article we will use the same setup of enclosing a circle inside a tight square. However instead of measuring the area of the circle and then solving the equation for π we will start throwing random darts at the target!
Math
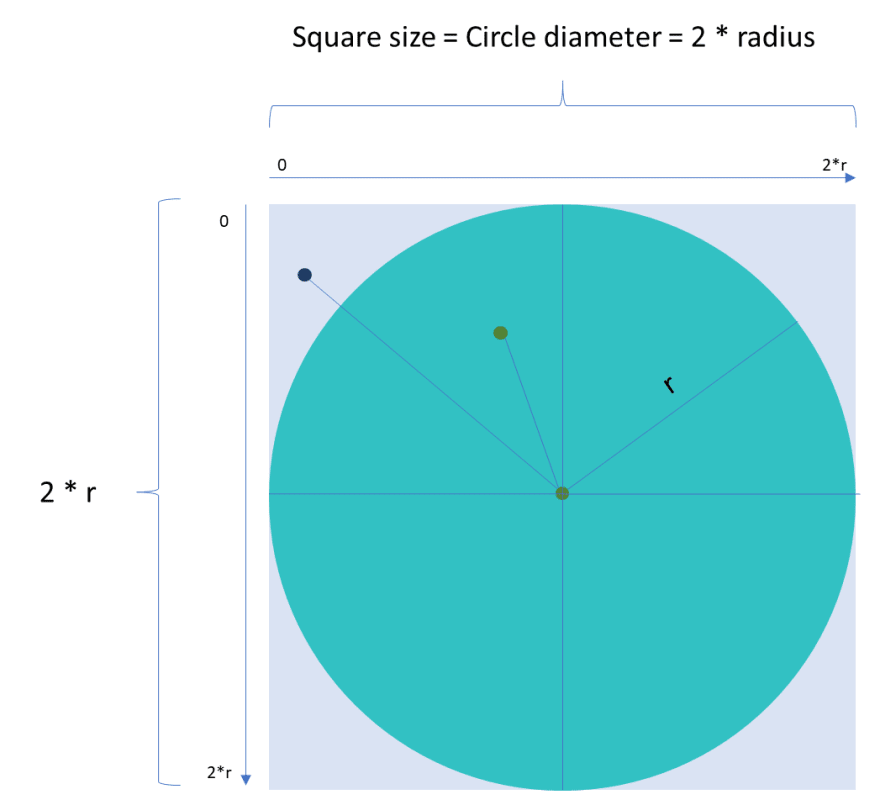
Before we start our implementation let’s do a little bit of math. Look at the previous picture and notice that:
Area square = 4r²
Area circle = πr²
By solving these equations for π we will find out that:
π = 4 * Area circle / Area square
The catch is no not calculate areas by mathematical means, but instead randomly throw darts towards the canvas… which after a while we expect to cover the entire area of square and of course circle.
Algorithm
Let’s put the above observation is an algorithm:
- Step 1: Throw random darts at the target. We will assume we have a good enough aim and all the darts will hit at least the square.
- Step 2: Count how many darts we throw in total (e.g. totalPoints)
- Step 3: Count how many darts are falling in the circle (e.g. circlePoints)
- Step 4: Calculate π by using formula π = (4 * circlePoints) / totalPoints
Of course, throwing darts is a simple random operation that need to be repeated many, many times in order to get a relevant result.
Coding
Now we have all the data we need to start writing the JavaScript code that will calculate π.
You can use any JavaScript environment or playground to write the code. In this article we will use the free codeguppy.com environment (you just need to create a free account to use it).
Although we talked until now only about graphical concepts, the code won’t use any graphical library. We can implement this algorithm using only pure JavaScript without drawing circles or squares.
var p = calcPI();
println(p);
function calcPI()
{
var r = 100;
var side = r * 2;
var totalPoints = 10000;
var circlePoints = 0;
for(var i = 0; i < totalPoints; i++)
{
var x = randomNumber(0, side - 1);
var y = randomNumber(0, side - 1);
var d = dist(x, y, r, r);
if (d <= r)
{
circlePoints++;
}
}
// area_square = 4r²
// area_circle = πr²
// => π = 4 * area_circle / area_square
return (4 * circlePoints) / totalPoints;
}
If you copy the above code in the codeguppy.com editor and run it, you will see the result displayed:
3.1496
This will vary with each execution due to the random function used… but nevertheless notice that whatever result you’ll get will be pretty close to the actual π value, which is pretty incredible for such simple empirical method!
Note: Please notice that we didn’t defined the dist function that calculates the distance between two points. This is because this function is already defined in codeguppy.com. However, if you want to run the code outside codeguppy.com, then you can easily implement this function in just a few lines of code as explained in the previous article. Same with randomNumber.
We will leave the exercise of implementing dist and randomNumber functions to the interested readers who want to port the example outside codeguppy.com.
Visualizing the circle
As you saw there is no need to use any graphical library to calculate the π using this method. However, since we are in a graphical environment, let’s have a little bit of fun and visualize the points that we are scanning.
We will use the point function to plot the scanned point in either “teal” (if is inside the circle), or “lightblue” if is outside the circle.
Just add the following 3 lines in the right place:
...
if (d <= r)
{
circlePoints++;
stroke("blue");
}
else
{
stroke("pink");
}
point(x, y);
...
And this is the execution effect:
I hope you had fun with this exercise!
You can find a working example of this code in this playground: https://codeguppy.com/code.html?il9pKB98SL64ChHTMiwb
Happy coding!








Top comments (0)