As promised in my last post on recursion, which I recommend reading before this article as we will be using it a lot in my examples, I want to take a closer look at the tree data structure in this article. Trees are a non-sequential data structure that is useful for storing information that needs to be found easily. In other words, they are an abstract model of a hierarchical structure (think of a family tree). Trees consist of nodes with a parent-child relationship.

Binary Tree and Binary Search Tree

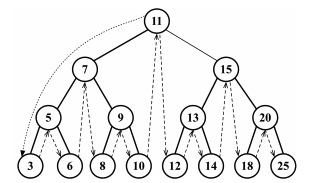
A node in a binary tree has at most two children: a left and a right child. This definition allows you to write algorithms to insert, search, and delete nodes more efficiently. Refer to the image above to see a binary tree and the key vocabulary that I will be using in this article.

As you can probably guess, a binary search tree (BST) is a binary tree. The key difference is that a BST only allows you to store nodes with lesser value on the left side and nodes with greater value on the right. In case you didn’t notice, this is exemplified in the image above. If you’re having a difficult time understanding how the image is ordered, don’t worry, we’ll go into more detail in the next sections!

Creating the Node and BST Classes

As usual, I highly encourage you to code along with me and to continuously test/play around with whatever we write. To start, we will create our Node class which will represent the nodes in our BST:

class Node {
    constructor(data) {
        this.data = data; // node value
        this.left = null;   // left node child reference
        this.right = null; // right node child reference
    }
}

Next, we will declare the basic structure of our BinarySearchTree class:

class BinarySearchTree {
    constructor() {
        this.root = null; // root of bst
    }
}

Our next step will be to implement some methods. Here’s what we’ll cover:

• insert(data)
• inOrderTraverse()
• preOrderTraverse()
• postOrderTraverse()
• search(data)
• remove(data)

Inserting a Node into a BST

To insert a new node into a tree, there are two steps we will follow:

1. Verify whether the insertion is a special case. In other words, we need to check if the node we are trying to add is the first one in a tree. If it is, we simply need to point the root to this new node by creating an instance of the Node class and assigning it to the root property.
2. Add the node to a different position than the root.

insert(data) {
    let newNode = new Node(data);

    if(this.root === null) {
        this.root = newNode;
    } else {
        this.insertNode(this.root, newNode); // helper method below
    }
}

insertNode(node, newNode) {
    if(newNode.data < node.data) {
        if(node.left === null) {
            node.left = newNode;
        } else {
            this.insertNode(node.left, newNode);
        }
    } else {
        if(node.right === null) {
            node.right = newNode;
        } else {
            this.insertNode(node.right, newNode);
        }
    }
}

To summarize, insert(data) creates a new Node with a value of data and if the tree is empty, it sets that node as the tree’s root, otherwise it calls insertNode(this.root, newNode). insertNode(node, newNode) is our helper method which is responsible for comparing the new node data with the data of the current node and moving left or right accordingly recursively until it finds a correct node with a null value where the new node can be added.

As an example, if we were to execute the following code...

const BST = new BinarySearchTree();
BST.insert(11); // establishes root node 
BST.insert(7);
BST.insert(9);
BST.insert(15);
...
BST.insert(6);

...we can illustrate the last insert with this diagram:

Traversing the BST

Traversing a tree is the process of visiting all the nodes in a tree and performing an operation at each node. The big question is, how should we go about this? There are three common approaches: in-order, pre-order, and post-order.

In-Order Traversal

An in-order traversal will visit all nodes in ascending order, starting from a given node (optional), and perform the given callback function (also optional). Again, we will use recursion here:

inOrderTraverse(node, callback) {
    if(node != null) {
        this.inOrderTraverse(node.left, callback);
        callback(node.data);
        this.inOrderTraverse(node.right, callback);
    }
}

The following diagram shows the path that our inOrderTraverse takes:

Pre-Order Traversal

A pre-order traversal visits the node prior to its descendants. Take note of the pretty subtle difference the the order in the code and in the diagram:

preOrderTraverse(node, callback) {
    if(node != null) {
        callback(node.data);
        this.preOrderTraverse(node.left, callback);
        this.preOrderTraverse(node.right, callback);
    }
}

Post-Order Traversal

If you haven't guessed already, a post-order traversal visits the node after its descendants. You can probably guess how the code will differ here but be sure to double check yourself with the diagram:

postOrderTraverse(node, callback) {
    if(node != null) {
        this.postOrderTraverse(node.left, callback);
        this.postOrderTraverse(node.right, callback);
        callback(node.data);
    }
}

Searching for Values in a BST

In our implementation, node represents the current node and data represents the value we are searching for:

search(node, data) {
    if(node === null) {
        return null;
    } else if(data < node.data) {
        return this.search(node.left, data);
    } else if(data > node.data) {
        return this.search(node.right, data);
    } else {
        return node;
    }
}

I encourage you to give test your code here and you can add in a console.log so you can see which nodes are visited. Even if you aren't coding along, go ahead and trace one of the diagrams in this article and predict the method's path when searching for a particular value. You'll notice how easy it is to find the max and min values too!

Removing a Node from a BST

The remove method is the most complex method we will cover in this article. It's complexity is due to the different scenarios that we need to handle and because it is recursive.

remove(data) {
    this.root = this.removeNode(this.root, data); // helper method below
}

removeNode(node, data) {
    if(node === null) {
        return null;
    // if data to be deleted is less than the root's data, move to the left subtree
    } else if(data < node.data) {
        node.left = this.removeNode(node.left, data);
        return node;
    // if data to be deleted is greater than the root's data, move to the right subtree
    } else if(data > node.data) {
        node.right = this.removeNode(node.right, data);
        return node;
    // if data is similar to the root's data, delete the node
    } else {
        // delete node with no children (leaf node)
        if(node.left === null && node.right === null) {
            node = null;
            return node;
        }

        // delete node with one child
        if(node.left === null) {
            node = node.right;
            return node;
        } else if(node.right === null) {
            node = node.left;
            return node;
        }

        // delete node with two children
        // minimum node of the right subtree is stored in newNode
        let newNode = this.minNode(node.right);
        node.data = newNode.data;
        node.right = this.removeNode(node.right, newNode.data);
        return node;
    }
}

If we end up finding the matching node to be deleted, there are three scenarios to handle which we will discuss in more detail below. These scenarios can be found in the big else statement in the code.

Removing a Leaf Node

The first scenario involves a leaf node which does not have a left or right child. In this case, we will need to remove the node by assigning null to it. However, don't forget that we will also want to take care of the references from the parent node. Refer to the diagram which shows the removal of a leaf node:

Removing a Node with One Child

The second scenario involves a node that has a left of right child. As you can see in the diagram below, we will need to skip matching node and assign the parent pointer to the child node:

Removing a Node with Two Children

The third and final scenario involves a node with both let and right children. To remove such a node, follow these steps:

1. Once you find the node to be removed, find the minimum node from its right edge subtree (refer to shaded area in the diagram below).
2. Next you can update the value of the node with the key of the minimum node from its right subtree. With this action, you are replacing the key of thenode, which means it is effectively removed.
3. Now you have two nodes in the tree with the same key which cannot happen (refer to the two 18s in the diagram). Thus, you need to remove the minimum node from the right subtree since you moved it to the place of the removed node.
4. Finally, return the updated node reference to its parent.

Conclusion

In this article, we covered the algorithms to add, search for, and remove nodes from a binary search tree as well as treee traversal.

For some additional fun, I came across this interesting tool where you can play around with an interactive BST along with many other data structures, created by David Galles. And if you want to learn more about the cover image and how it relates to binary trees, check out this explanation of symmetric binary trees by Larry Riddle (be warned it's pretty math heavy but there are some cool illustrations)!