Greetings fellow devs!
Hope you're doing well despite the whole pandemic situation and are staying healthy.
I wanted to write about this very interesting/difficult solution to a problem that I learned today.
Finding the duplicate number within an array/list.
Before anything, I would encourage you to take a look at the Leetcode problem statement.
And try to solve it. Doesn't matter if you can't do it. This is an extremely strange problem.
The given
- The list of nums contains n+1 integers.
- And each num within nums is of range, 1..n(inclusive).
- There is only one duplicate number in the list.
Different solutions
- Iterate through the list and sort it, and then find if two adjacent nums are equal and return one of those nums.
- Store the seen nums in another list, and then return num if the num is already in seen.
Also, follow up note to the problem
- Space complexity should be O(1) - constant space.
- Time complexity should be less than O(n^2).
Whew, okay. On to the solutions that match the follow-up note.
I did see binary search being listed as a solution, probably to reduce time complexity by half(so O(log n)) with constant space complexity. But I was more interested in another solution and that was a bit challenging. Somehow, it took me about a day to understand this.
nums = [2,6,4,1,3,1,5]
Output - 1
The idea is to have two pointers - slow and fast. These would move through the list by using the current number as the index to the next element to iterate through. And as always, fast moves two steps ahead of slow. The iterations would create a linked list that contains a cycle due to the duplicate element.
So, this problem is being transformed into the problem of finding a cycle within a linked list.
The new problem statement
Given a linked list, find the entrance node/ element of the cycle.
Why should we find the starting point of the cycle?
Read on.
Constructing our linked list
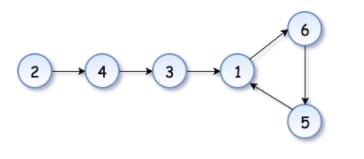
We would now find the sequence of numbers by iterating through nums(given above) and creating a linked list. The duplicate would have the same value and link back to the original value thus creating the cycle. The explanation of how each next number is identified is mentioned in () next to the number.
[2,6,4,1,3,1,5]
You start from the first element.
2 -> 4(nums[2]) -> 3(nums[4]) -> 1(nums[3]) -> 6(nums[1]) -> 5(nums[6]) -> 1(nums[5]) -> 6(nums[1]) -> 5(nums[6]) -> 1(nums[5]) -> ....
And that sequence just goes on. That's a cycle. When we see that, we would be like, damn, now where does that cycle start!?
Okay, fine, let's first construct a visual aid of a linked list from this.
Thanks to Leetcode, we have it here.
Now for the approach
The duplicate element is the entrance of a cycle present within the list of numbers. Wait, whaaaat?
Two steps
Find if there's a loop- while iterating through the list, if at some point, both theslowandfastpointers are pointing to the same node, then yes, a loop is present. Sincefastis moving two nodes ahead,fastandslowwould point to the same node only if there is a loop.Find the starting node of the cycle.
How do we do this?
Also, since we found an node where both fast and slow point to, couldn't we just return that?
Well, no.
Why?
The intersection node is not necessarily the duplicate element/node as this intersection node is a node in the cycle where the fast caught up with the slow or where the fast and slow pointers randomly met - this just proves that there's a cycle in the linked list.
To get the exact duplicate element, we need to see where this loop/cycle originated.
To find this origin, we need to push the slow pointer to the start of the list and move both fast and slow pointers at the same rate, one at a time, and when they now meet at the same node, that is the start of the cycle/loop.
Some math-ish stuff
Assuming D = the number of steps/distance from the start of the linked list to the start of the cycle and K = the number of steps/distance from the start of the cycle to the intersection point we determined in Step 1. Since slow moves to the start(0), its position after D steps is D. The fast pointer continues from the intersection point, so its position after D steps would be, nC(some number of cycles) - K, which is equal to D => nC - K = D.
Now, we got that cleared away, time to finally code this up!
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
slow = nums[0]
fast = nums[0]
while True:
slow = nums[slow]
fast = nums[nums[fast]]
if slow == fast:
break
slow = nums[0]
while slow != fast:
slow = nums[slow]
fast = nums[fast]
return fast
Resources to go through if you're stuck during the struggle of understanding this solution
- Gaurav Sen's awesome video on finding the start of the cycle in the linked list. Watch this at least twice and you'll understand.
- Floyd's cycle detection algorithm on Wikipedia.
- This really cool solution.
- Nick White's video to understand that even cool YouTubers struggle with this problem.
- Also, it's very important to understand the difference between finding whether a cycle/loop exists in the linked list and finding where the entry/starting node of the cycle is.
- Also, this StackOverflow answer is the source of a lot of answers to the questions during the learning process.
- Of course, look at the Leetcode solution explanation.
Thank you so much for reading. This solution to the problem was a tough one to understand, soo, if you are stuck in the learning process (I was too!), do let me know, maybe I can help.






Top comments (0)