Bryan C Guner

Posted on Jul 16, 2021

Quick Guide To Big O

A Quick Guide to Big-O Notation, Memoization, Tabulation, and Sorting Algorithms by Example

Curating Complexity: A Guide to Big-O Notation

A Quick Guide to Big-O Notation, Memoization, Tabulation, and Sorting Algorithms by Example

Curating Complexity: A Guide to Big-O Notation

Medium-article-comp-complex

A Node.js repl by bgoonzreplit.com

Why is looking at runtime not a reliable method of calculating time complexity?
Not all computers are made equal( some may be stronger and therefore boost our runtime speed )
How many background processes ran concurrently with our program that was being tested?
We also need to ask if our code remains performant if we increase the size of the input.
The real question we need to answering is: How does our performance scale?.

big ‘O’ notation

Big O Notation is a tool for describing the efficiency of algorithms with respect to the size of the input arguments.
Since we use mathematical functions in Big-O, there are a few big picture ideas that we’ll want to keep in mind:
The function should be defined by the size of the input.
Smaller Big O is better (lower time complexity)
Big O is used to describe the worst case scenario.
Big O is simplified to show only its most dominant mathematical term.

Simplifying Math Terms

We can use the following rules to simplify the our Big O functions:
Simplify Products : If the function is a product of many terms, we drop the terms that don't depend on n.
Simplify Sums : If the function is a sum of many terms, we drop the non-dominant terms.
n : size of the input
T(f) : unsimplified math function
O(f) : simplified math function.

Putting it all together

- First we apply the product rule to drop all constants.

Then we apply the sum rule to select the single most dominant term.

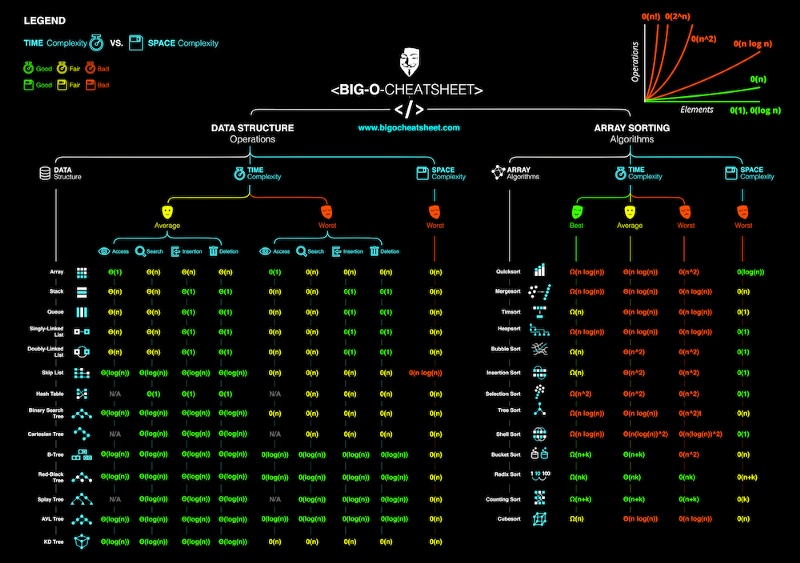
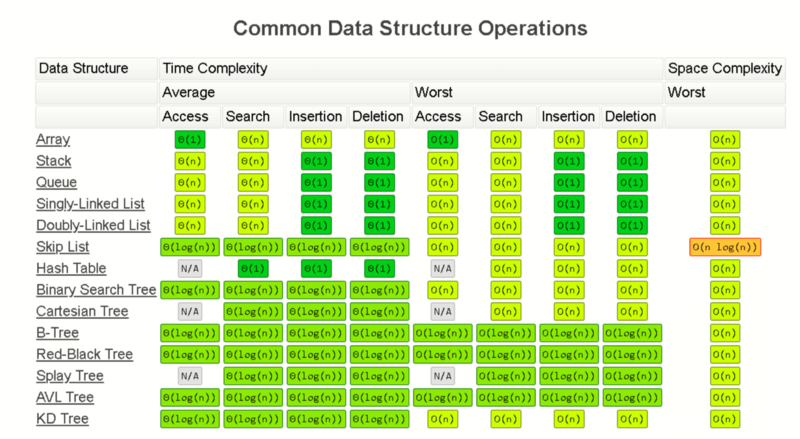
Complexity Classes

Common Complexity Classes

There are 7 major classes in Time Complexity

#### O(1) Constant

The algorithm takes roughly the same number of steps for any input size.

`O(log(n)) Logarithmic`

In most cases our hidden base of Logarithmic time is 2, log complexity algorithm’s will typically display ‘halving’ the size of the input (like binary search!)

`O(n) Linear`

Linear algorithm’s will access each item of the input “once”.

`O(nlog(n)) Log Linear Time`

Combination of linear and logarithmic behavior, we will see features from both classes.

Algorithm’s that are log-linear will use both recursion AND iteration.

`O(nc) Polynomial`

C is a fixed constant.

`O(c^n) Exponential`

C is now the number of recursive calls made in each stack frame.

Algorithm’s with exponential time are VERY SLOW.

Memoization

Memoization : a design pattern used to reduce the overall number of calculations that can occur in algorithms that use recursive strategies to solve.
MZ stores the results of the sub-problems in some other data structure, so that we can avoid duplicate calculations and only ‘solve’ each problem once.
Two features that comprise memoization:

FUNCTION MUST BE RECURSIVE.
Our additional Data Structure is usually an object (we refer to it as our memo… or sometimes cache!)

### Memoizing Factorial

Our memo object is mapping out our arguments of factorial to it’s return value.

Keep in mind we didn’t improve the speed of our algorithm.

Memoizing Fibonacci

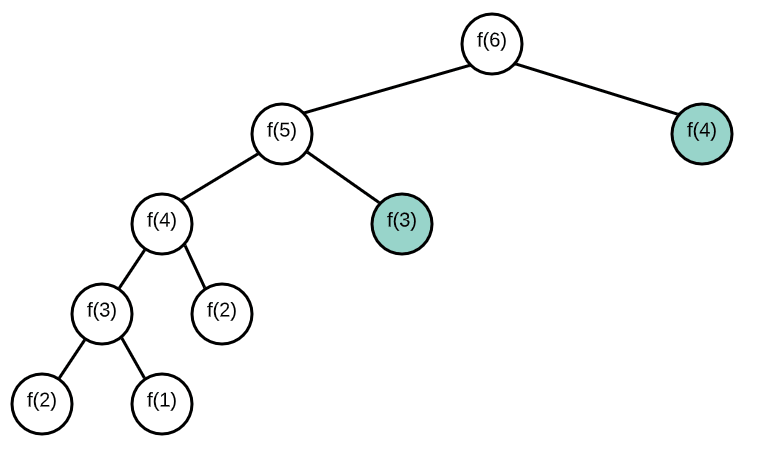
- Our time complexity for Fibonacci goes from O(2^n) to O(n) after applying memoization.

The Memoization Formula

Rules:

Write the unoptimized brute force recursion (make sure it works);
Add memo object as an additional argument .
Add a base case condition that returns the stored value if the function’s argument is in the memo.
Before returning the result of the recursive case, store it in the memo as a value and make the function’s argument it’s key.

Things to remember

When solving DP problems with Memoization, it is helpful to draw out the visual tree first.
When you notice duplicate sub-tree’s that means we can memoize.

Tabulation

Tabulation Strategy

Use When:

The function is iterative and not recursive.
The accompanying DS is usually an array.

Steps for tabulation

Create a table array based off the size of the input.
Initialize some values in the table to ‘answer’ the trivially small subproblem.
Iterate through the array and fill in the remaining entries.
Your final answer is usually the last entry in the table.

Memo and Tab Demo with Fibonacci

Normal Recursive Fibonacci

function fibonacci(n) {
  if (n <= 2) return 1;
  return fibonacci(n - 1) + fibonacci(n - 2);
}

Memoization Fibonacci 1

Memoization Fibonacci 2

Tabulated Fibonacci

Example of Linear Search

Worst Case Scenario: The term does not even exist in the array.
Meaning: If it doesn’t exist then our for loop would run until the end therefore making our time complexity O(n).

Sorting Algorithms

Bubble Sort

Time Complexity: Quadratic O(n^2)

The inner for-loop contributes to O(n), however in a worst case scenario the while loop will need to run n times before bringing all n elements to their final resting spot.

Space Complexity: O(1)

Bubble Sort will always use the same amount of memory regardless of n.

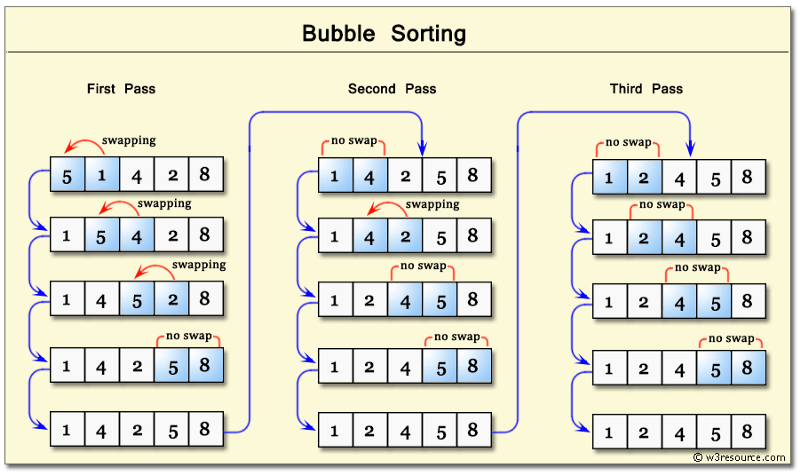
- The first major sorting algorithm one learns in introductory programming courses.

Gives an intro on how to convert unsorted data into sorted data.

It’s almost never used in production code because:

It’s not efficient
It’s not commonly used
There is stigma attached to it
Bubbling Up : Term that infers that an item is in motion, moving in some direction, and has some final resting destination.
Bubble sort, sorts an array of integers by bubbling the largest integer to the top.

Worst Case & Best Case are always the same because it makes nested loops.
Double for loops are polynomial time complexity or more specifically in this case Quadratic (Big O) of: O(n²)

Selection Sort

Time Complexity: Quadratic O(n^2)

Our outer loop will contribute O(n) while the inner loop will contribute O(n / 2) on average. Because our loops are nested we will get O(n²);

Space Complexity: O(1)

Selection Sort will always use the same amount of memory regardless of n.

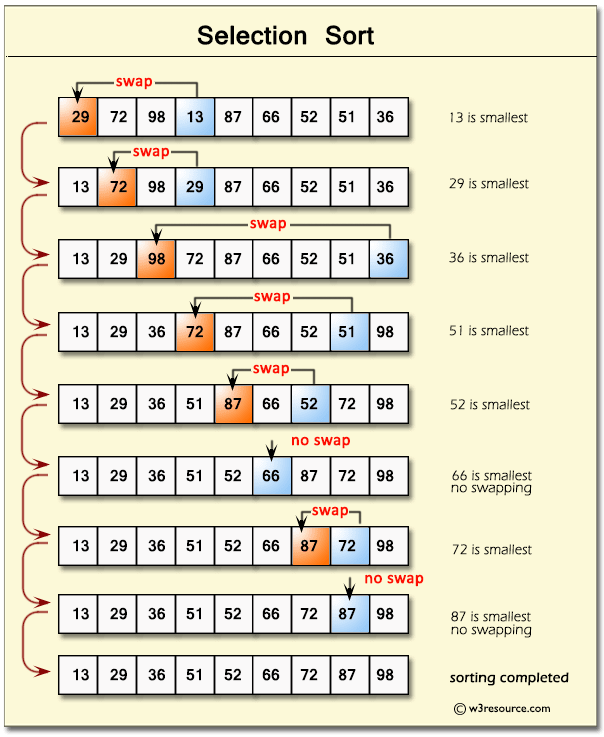
- Selection sort organizes the smallest elements to the start of the array.

Summary of how Selection Sort should work:

Set MIN to location 0
Search the minimum element in the list.
Swap with value at location Min
Increment Min to point to next element.
Repeat until list is sorted.

Insertion Sort

Time Complexity: Quadratic O(n^2)

Our outer loop will contribute O(n) while the inner loop will contribute O(n / 2) on average. Because our loops are nested we will get O(n²);

Space Complexity: O(n)

Because we are creating a subArray for each element in the original input, our Space Comlexity becomes linear.

### Merge Sort

Time Complexity: Log Linear O(nlog(n))

Since our array gets split in half every single time we contribute O(log(n)). The while loop contained in our helper merge function contributes O(n) therefore our time complexity is O(nlog(n)); Space Complexity: O(n)
We are linear O(n) time because we are creating subArrays.

### Example of Merge Sort

- Merge sort is O(nlog(n)) time.

We need a function for merging and a function for sorting.

Steps:

If there is only one element in the list, it is already sorted; return the array.
Otherwise, divide the list recursively into two halves until it can no longer be divided.
Merge the smallest lists into new list in a sorted order.

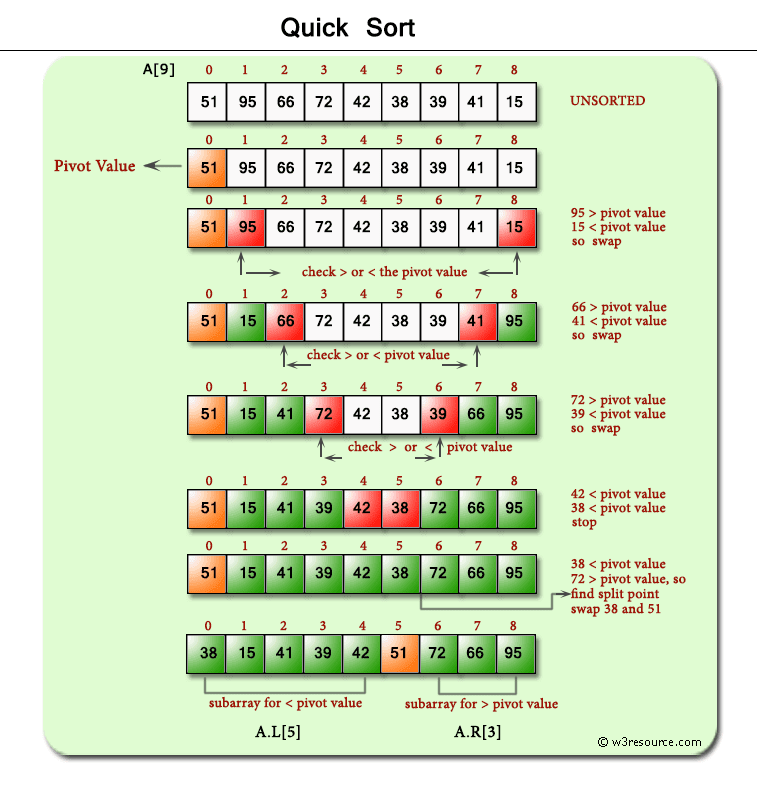
Quick Sort

Time Complexity: Quadratic O(n^2)

Even though the average time complexity O(nLog(n)), the worst case scenario is always quadratic.

Space Complexity: O(n)

Our space complexity is linear O(n) because of the partition arrays we create.
QS is another Divide and Conquer strategy.
Some key ideas to keep in mind:
It is easy to sort elements of an array relative to a particular target value.
An array of 0 or 1 elements is already trivially sorted.

### Binary Search

Time Complexity: Log Time O(log(n))

Space Complexity: O(1)

Recursive Solution

Min Max Solution

Must be conducted on a sorted array.
Binary search is logarithmic time, not exponential b/c n is cut down by two, not growing.
Binary Search is part of Divide and Conquer.

Insertion Sort

Works by building a larger and larger sorted region at the left-most end of the array.

Steps:

If it is the first element, and it is already sorted; return 1.
Pick next element.
Compare with all elements in the sorted sub list
Shift all the elements in the sorted sub list that is greater than the value to be sorted.
Insert the value
Repeat until list is sorted.