Big O
function factorial(n) {
if (n === 1) return 1;
return n * factorial(n - 1);
}
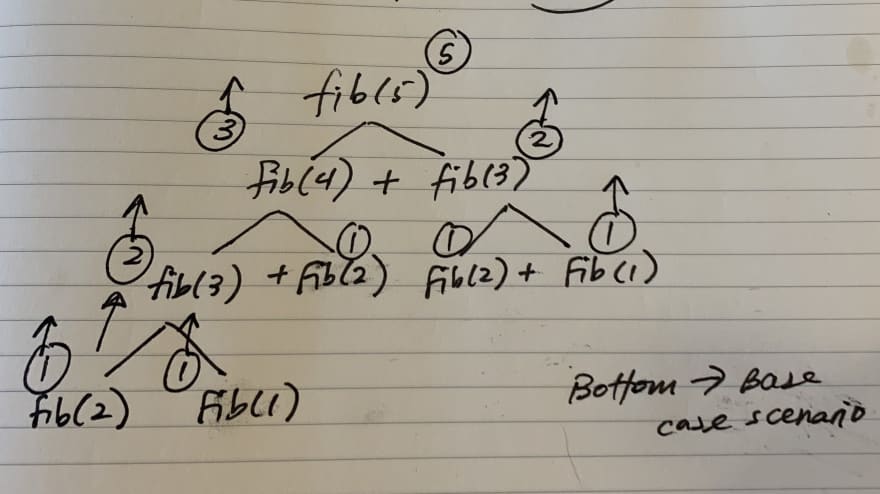
function fibonacci(n) {
if (n === 1 || n === 2) return 1;
return fib(n - 1) + fib(n - 2);
}
Big O Notation
-
Big O helps gives us a precise vocabulary to talk about how our code performs.
- Useful for discussing trade-offs between different approaches.
- Helps us debug things easier.
- It also comes up a lot in interviews!
An Example: Comparing two functions that calculate the sum of all numbers from 1 up to n.
function addUpTo(n) {
let total = 0;
for (let i = 0; i <= n; i++) {
total += i;
}
return total;
}
Number of operations will grow with n.
Would be O(n) or Linear Time.
function addUpTo(n) {
return (n * (n + 1)) / 2;
}
Has three simple operations: 1 Multiplication 1 Addition 1 Division. (Regardless of n)
Would be O(1) or Constant Time.
-
First we need to consider what makes one implementation better than the other?
- Faster? (Time Complexity);
- Less Memory Intensive (Space Complexity);
- More Readable
-
How can we measure speed?
- Timers? (Doesn't work well - not reliable or precise)
- Instead we should count the number of simple operations.
Big O Notation is a way to formalize fuzzy counting.
-
An algorithm is O(f(n)) if the number of simple operations the computer has to do is eventually less than a constant f(n) times, as n increases.
- f(n) = n (Linear)
- f(n) = n^2 (Quadratic)
- f(n) = 1 (Constant)
- f(n) could be anything!
function countUpAndDown(n) {
console.log('going up!');
for (let i = 0; i < n; i++) {
console.log(i);
}
console.log('at the top, going down!');
for (let j = n - 1; j >=0; j--) {
console.log(j);
}
console.log('Back down, bye!);
}
Both loops are O(n) but since we just want the big picture, this entire function would be O(n);
function printAllPairs(n) {
for (var i = 0; i < n; i++) {
for (var j = 0; j < n; j++) {
console.log(i, j);
}
}
}
Nested loops are never a good thing when trying to write fast code.
O(n^2) or Quadratic Time.
-
Constants don't matter in big O & Smaller Terms don't matter
- O(2n) is just O(n) Linear
- O(500) is just O(1) Constnat
- O(13n^2) is just O(n^2) Quadratic
- O(n + 10) is just O(n) Linear
- O(1000n + 50) is just O(n) Linear
- O(n^2 + 5n + 8) is just O(n^2) Quadratic
-
Big O Shorthands- Arithmetic Operations are Constant
- Variable assignment is constant
- Accessing elements in an array (by index) or by object (by key) is constant.
- In a loop, the complexity is the length of the loop times the complexity of whatever is inside of the loop.
Additional Examples
function logAtLeast5(n) {
for (var i = 1; i <= Math.max(5, n); i++) {
console.log(i);
}
}
O(n) Linear Time
function logAtMost5(n) {
for (var i = 1; i <= Math.min(5, n); i++) {
console.log(i);
}
}
O(1) Constant Time.
A Guide to Big-O Notation
Curating Complexity: A Guide to Big-O Notation
-
Why is looking at runtime not a reliable method of calculating time complexity?
- Not all computers are made equal( some may be stronger and therefore boost our runtime speed )
- How many background processes ran concurrently with our program that was being tested?
- We also need to ask if our code remains performant if we increase the size of the input.
The real question we need to answering is:
How does our performance scale?.
Big O Notation
- Big O Notation is a tool for describing the efficiency of algorithms with respect to the size of the input arguments.
- Since we use mathematical functions in Big-O, there are a few big picture ideas that we'll want to keep in mind:
- The function should be defined by the size of the input.
-
SmallerBig O is better (lower time complexity) - Big O is used to describe the worst case scenario.
- Big O is simplified to show only its most dominant mathematical term.
Simplifying Math Terms
-
We can use the following rules to simplify the our Big O functions:
-
Simplify Products: If the function is a product of many terms, we drop the terms that don't depend on n. -
Simplify Sums: If the function is a sum of many terms, we drop the non-dominant terms.
-
n: size of the inputT(f): unsimplified math functionO(f): simplified math function.
Simplifying a Product
| Unsimplified | Big-O Simplified |
| ------------ | ---------------- |
| T(5 _ n^2) | O(n^2) Quadratic |
| T(100000 _ n) | O(n) Linear |
| T( n / 12) | O (n) Linear |
| T( 42 _ n _ log(n)) | O(nlog(n)) Log Linear |
| T(12) | O(1) Constant |
Simplifying a Sum
| Unsimplified | Big-O Simplified |
| ------------ | ---------------- |
| T( n3 + n2 + n ) | O(n^3) |
| T( log(n) + 2n )| O(2^n) Exponential |
| T( n + log(n) ) | O(n) Linear |
| T( n! + 10n ) | O(n!) Polynomial |
Putting it all together
| Unsimplified | Big-O Simplified |
|---|---|
| T( 5n2 + 99n ) | O(n^2) Quadratic |
| T( 2n + nlog(n) ) | O(nlog(n)) Log Linear |
| T( 2n + 5n1000) | O(2^n) Exponential |
- First we apply the product rule to drop all constants.
- Then we apply the sum rule to select the single most dominant term.
Complexity Classes
Common Complexity Classes
There are 7 major classes in Time Complexity
| Big O | Complexity Class Name |
|---|---|
| O(1) | Constant |
| O(log(n)) | Logarithmic |
| O(n) | Linear |
| O(nlog(n)) | Loglinear, Linearithmetic, Quasilinear |
| O(nc) - O(n2), O(n3), etc. | Polynomial |
| O(cn) - O(2n), O(3n), etc. | Exponential |
| O(n!) | Factorial |
-
O(1) Constant- The algorithm takes roughly the same number of steps for any input size.
// O(1)
function constant1(n) {
return n * 2 + 1;
}
// O(1)
function constant2(n) {
for (let i = 1; i <= 100; i++) {
console.log(i);
}
}
-
O(log(n)) Logarithmic- In most cases our hidden base of Logarithmic time is 2, log complexity algo's will typically display 'halving' the size of the input (like binary search!)
// O(log(n))
function logarithmic1(n) {
if (n <= 1) return;
logarithmic1(n / 2);
}
// O(log(n))
function logarithmic2(n) {
let i = n;
while (i > 1) {
i /= 2;
}
}
-
O(n) Linear- Linear algo's will access each item of the input "once".
// O(n)
function linear1(n) {
for (let i = 1; i <= n; i++) {
console.log(i);
}
}
// O(n), where n is the length of the array
function linear2(array) {
for (let i = 0; i < array.length; i++) {
console.log(i);
}
}
// O(n)
function linear3(n) {
if (n === 1) return;
linear3(n - 1);
}
-
O(nlog(n)) Log Linear Time- Combination of linear and logarithmic behavior, we will see features from both classes.
- Algo's that are log-linear will use both recursion AND iteration.
// O(n * log(n))
function loglinear(n) {
if (n <= 1) return;
for (let i = 1; i <= n; i++) {
console.log(i);
}
loglinear(n / 2);
loglinear(n / 2);
}
-
O(nc) Polynomial- C is a fixed constant.
// O(n^2)
function quadratic(n) {
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {}
}
}
// O(n^3)
function cubic(n) {
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {
for (let k = 1; k <= n; k++) {}
}
}
}
Example of Quadratic and Cubic runtime.
-
O(c^n) Exponential- C is now the number of recursive calls made in each stack frame.
- Algo's with exponential time are VERY SLOW.
// O(2^n)
function exponential2n(n) {
if (n === 1) return;
exponential_2n(n - 1);
exponential_2n(n - 1);
}
// O(3^n)
function exponential3n(n) {
if (n === 0) return;
exponential_3n(n - 1);
exponential_3n(n - 1);
exponential_3n(n - 1);
}
-
O(n!) Factorial- The largest/ worst complexity (minus DTIME which is n^n);
Memoization
-
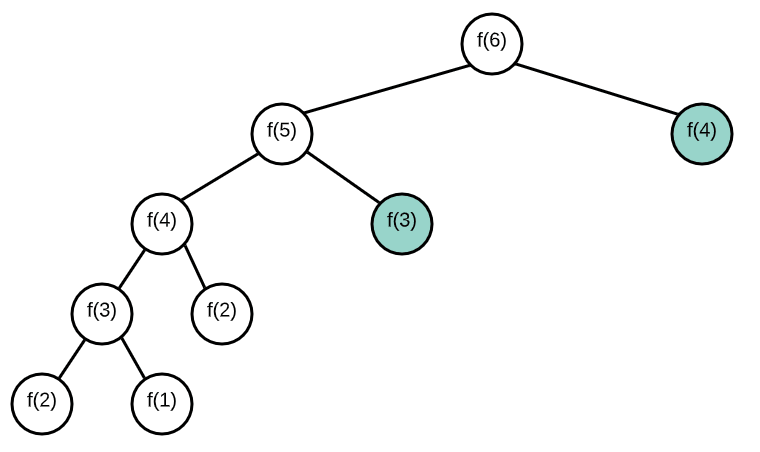
Memoization : a design pattern used to reduce the overall number of calculations that can occur in algorithms that use recursive strategies to solve.
- MZ stores the results of the sub-problems in some other data structure, so that we can avoid duplicate calculations and only 'solve' each problem once.
- Two features that comprise memoization:
- 1. FUNCTION MUST BE RECURSIVE.
- 2. Our additional DS is usually an object (we refer to it as our memo!)
Memoizing Factorial
let memo = {};
function factorial(n) {
// if this function has calculated factorial(n) previously,
// fetch the stored result in memo
if (n in memo) return memo[n];
if (n === 1) return 1;
// otherwise, it havs not calculated factorial(n) previously,
// so calculate it now, but store the result in case it is
// needed again in the future
memo[n] = n * factorial(n - 1);
return memo[n];
}
factorial(6); // => 720, requires 6 calls
factorial(6); // => 720, requires 1 call
factorial(5); // => 120, requires 1 call
factorial(7); // => 5040, requires 2 calls
memo; // => { '2': 2, '3': 6, '4': 24, '5': 120, '6': 720, '7': 5040 }
- Our memo object is mapping out our arguments of factorial to it's return value.
- Keep in mind we didn't improve the speed of our algo.
- Our time complexity for fibonacci goes from O(2^n) to O(n) after applying memoization.
The Memoization Formula
Rules
- Write the unoptimized brute force recursion (make sure it works);
- Add memo object as an additional arugmnt .
- Add a base case condition that returns the stored value if the function's argument is in the memo.
- Before returning the result of the recursive case, store it in the memo as a value and make the function's argument it's key.
Things to remember
- When solving DP problems with Memoization, it is helpful to draw out the visual tree first.
- When you notice duplicate sub-tree's that means we can memoize.
**
function fastFib(n, memo = {}) {
if (n in memo) return memo[n];
if (n === 1 || n === 2) return 1;
memo[n] = fastFib(n - 1, memo) + fastFib(n - 2, memo);
return memo[n];
}
fastFib(6); // => 8
fastFib(50); // => 12586269025
Tabulation
-
Tabulation Strategy
- Use When:
- The function is iterative and not recursive.
- The accompanying DS is usually an array.
function fib(n) {
let mostRecentCalcs = [0, 1];
if (n === 0) return mostRecentCalcs[0];
for (let i = 2; i <= n; i++) {
const [secondLast, last] = mostRecentCalcs;
mostRecentCalcs = [last, secondLast + last];
}
return mostRecentCalcs[1];
}
- Steps for tabulation
- Create a table array based off the size of the input.
- Initialize some values in the table to 'answer' the trivially small subproblem.
- Iterate through the array and fill in the remaining entries.
- Your final answer is usually the last entry in the table.
Class Examples
Example of Linear Search
function search(array, term) {
for (let i = 0; i < array.length; i++) {
if (array[i] === term) {
return i;
}
}
return -1;
}
- Worst Case Scenario: The term does not even exist in the array.
- Meaning: If it doesn't exist then our for loop would run until the end therefore making our time complexity O(n).
Example of Binary Search
function binarySearch(arr, x, start, end) {
if (start > end) return false;
let mid = Math.floor((start + end) / 2);
if (arr[mid] === x) return true;
if (arr[mid] > x) {
return binarySearch(arr, x, start, mid - 1);
} else {
return binarySearch(arr, x, mid + 1, end);
}
}
- Must be conducted on a sorted array.
- Binary search is logarithmic time, not exponential b/c n is cut down by two, not growing.
- Binary Search is part of Divide and Conquer.
Example of Merge Sort
function merge(leftArray, rightArray) {
const sorted = [];
while (letArray.length > 0 && rightArray.length > 0) {
const leftItem = leftArray[0];
const rightItem = rightArray[0];
if (leftItem > rightItem) {
sorted.push(rightItem);
rightArray.shift();
} else {
sorted.push(leftItem);
leftArray.shift();
}
}
while (leftArray.length !== 0) {
const value = leftArray.shift();
sorted.push(value);
}
while (rightArray.length !== 0) {
const value = rightArray.shift();
sorted.push(value);
}
return sorted;
}
function mergeSort(array) {
const length = array.length;
if (length === 1) {
return array;
}
const middleIndex = Math.ceil(length / 2);
const leftArray = array.slice(0, middleIndex);
const rightArray = array.slice(middleIndex, length);
leftArray = mergeSort(leftArray);
rightArray = mergeSort(rightArray);
return merge(leftArray, rightArray);
}
Example of Bubble Sort
function bubbleSort(items) {
var length = items.length;
for (var i = 0; i < length; i++) {
for (var j = 0; j < length - i - 1; j++) {
if (items[j] > items[j + 1]) {
var tmp = items[j];
items[j] = items[j + 1];
items[j + 1] = tmp;
}
}
}
}
- Worst Case & Best Case are always the same because it makes nested loops.
- Double for loops are polynomial time complexity or more specifically in this case Quadratic big O O(n^2);


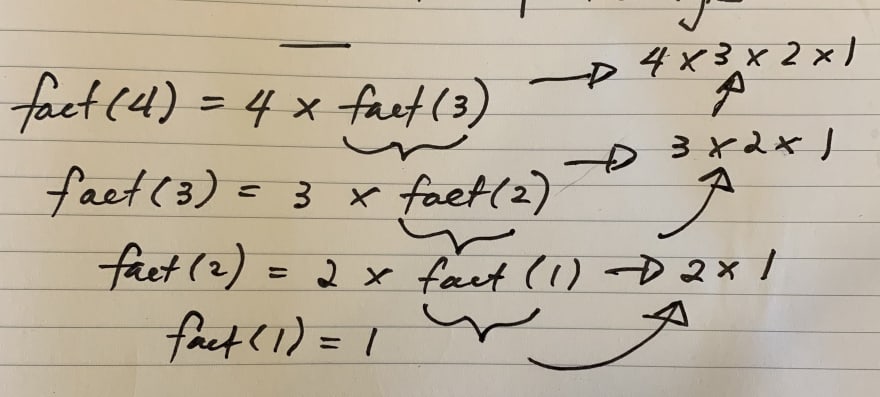

Top comments (0)