A Developer Boy and His Bubble Sort

Header image: Photo by Braedon McLeod on Unsplash

First Impression

I've learned about bubble sort recently. To my surprise, my initial impression of the term is not how the algorithm is at all. I thought it has to do with separating elements into bubbled zones so you'd know what to expect when looking into each zone.

Nope.

Break Down

It's called bubble sort because the largest element will "bubble" to the top (end). It can also be referred to as "sinking sort". Both names is not very intuitive to me, but what draws me in is how it works.

The basics of this algorithm is that it will go through an array n amount of times. Where n represents the array size. It will look at each element (current) and the element one index ahead (next). If the current is larger than the next, it will swap them. Regardless of the swap, it increment the current and next indices by 1 until it reaches the end.

In the next iteration, it will only look at the beginning through one element less than the last. For example:

• Your array size is 5
• First iteration will be index 0-4
• Swaps happens
• Second iteration will be index 0-3
• Swaps don't happen because it is all sorted, this also gets flagged
• Loops break and algorithm ends by returning the sorted array

Note: Swapping could also happen in the second, third, fourth iteration, etc... Then, the algorithm would keep going.

Here it is in action:

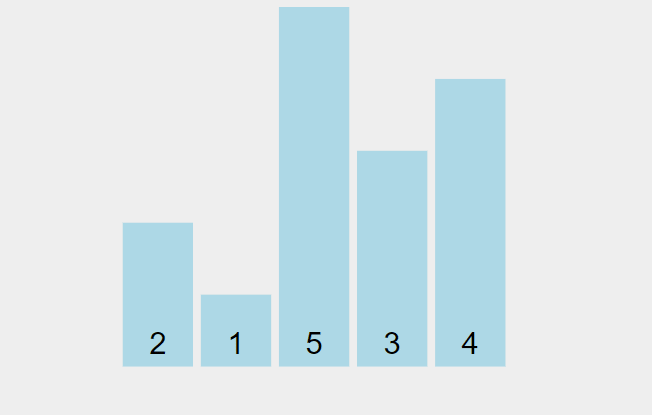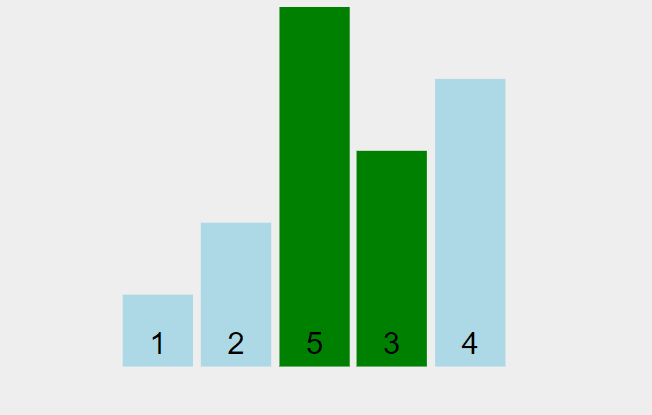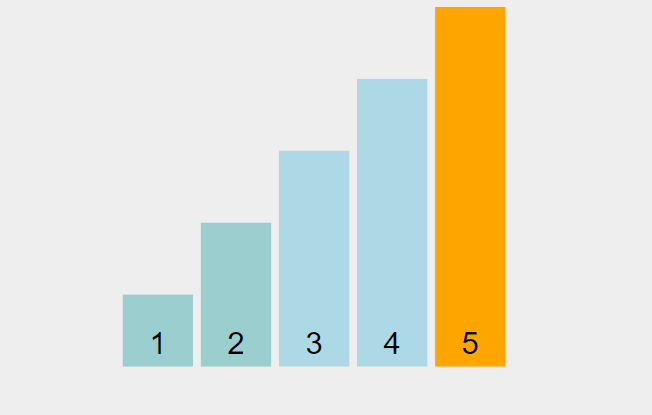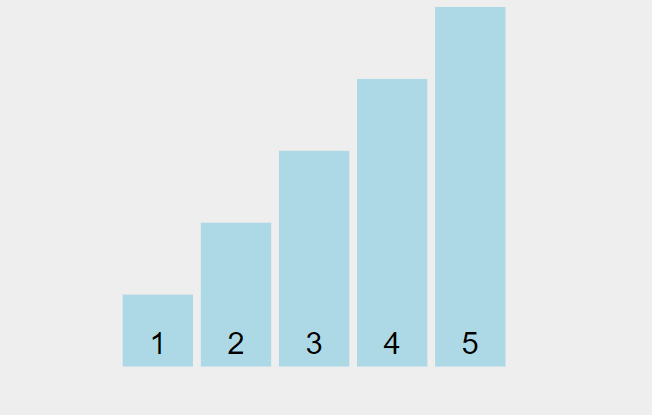
via visualgo.net

There's an advance logic added in what is shown. The algorithm will stop iterating if, after one run through, no swaps are made. This means that the array is already sorted, so we don't need to waste more runtime iterating the full n amount.

Why?

Bubble Sort is good for

• small data set
• semi-sorted arrays
• O(N) run time best case, O(N^2) worst case

The Components

We will need a helper function to swap two elements of an array:

function swapValues(array, i, j) {
    [array[i], array[j]] = [array[j], array[i]]
}

Here, we're reassigning the elements at index i and j in one line. You can also do it with 3 lines:

function swapValues(array, i, j) {
    let temp = array[i]
    array[i] = array[j]
    array[j] = temp
}

Next, we need two loops--nested. The outer loop will repeat the iteration n amount of times. The inner will look at each element and the one ahead of it. We will use a while outer and for inner here.
Note: Two for loops are fine, too

function bubbleSort(array) {
    let k = array.length

    while (k > 0) {
        for (let i = 0; i < k; i++) {
            //elements gets compared in here
        }

        //decrement k at the end for next iteration
        k--
    }
    return array
}

Execution

Add logic to compare two adjacent elements:

function bubbleSort(array) {
    let k = array.length

    while (k > 0) {
        for (let i = 0; i < k; i++) {
            //elements gets compared in here
            let j = i + 1
            if (array[i] > array[j]) {
                swapValues(array, i, j)
            }
            //add logic to break if no swaps happened
        }
        //decrement k at the end for next iteration
        k--
    }
    return array
}

If current element at i is greater than the next at j, we swap them. Now we add logic to break the loop if no swaps happened (AKA array is finish sorting before k runs out):

function bubbleSort(array) {
    let k = array.length

    while (k > 0) {
        //declare a noSwap boolean flag, assume true
        let noSwap = true
        for (let i = 0; i < k; i++) {
            //elements gets compared in here
            let j = i + 1
            if (array[i] > array[j]) {
                //if a swap happens, this iteration is flagged false, and next iteration needs to run through to check if array is sorted
                noSwap = false
                swapValues(array, i, j)
            }
            //add logic to break if no swaps happened
            //if the for loop completed with no swapping, the array is sorted
            if (noSwap) break
        }
        //decrement k at the end for next iteration
        k--
    }
    return array
}

That is the core of a bubble sort algorithm. You could also implement the swapValues logic directly as well, without a helper function.

Next up: Applying this algorithm to a HackerRank challenge!