In this Blog, we will discuss the Selection Sort Algorithm and its working procedure. Selection sort is an in-place comparison-based sorting algorithm that sorts the array by repeatedly finding and swapping the minimum element with the leftmost element of the array.
In-place means that the algorithm does not use extra space for manipulating the input but may require a small though non-constant extra space for its operation. Usually, this space is O(log n), though sometimes anything in O(n) (Smaller than linear) is allowed.
In this algorithm, the array is divided into two parts. One part will initially be empty but will contain the sorted array and is placed on the left-hand side, while the other part carries the original unsorted array and is placed on the right-hand side. In every iteration, the minimum element is picked from the unsorted list and gets placed at the beginning of the sorted array, thus reducing the size of the unsorted array by one while at the same time increasing the size of the sorted array by 1.
Now that we have understood what selection sort is, let’s understand its working procedure with a simple example of an array with a length of 5.
How Selection Sort Algorithm Works
The working principle of this algorithm is very simple. As told, we just have to find the minimum element from the unsorted array and place it at the beginning of the sorted array.
To begin with we have to assume that the first element of the unsorted subarray is the minimum element of the array. Then by iterating and comparing every element of this unsorted array with the first element which we have assumed to be the minimum element of the array we have to find the minimum element of the array.
If we find any element less than our current min element, that element becomes the new min of the array and the journey continues till the last element. Upon reaching the end of the array, simply replace the leftmost element of the unsorted array with the current min element. We have to do this every time until the array is sorted completely.
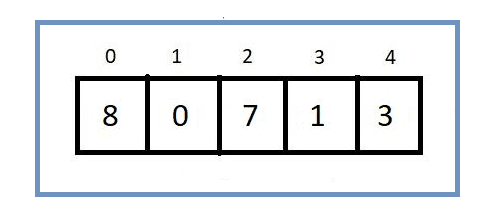
Let’s take an example of an array of length 5 to understand it better
Since the array we are using is of length 5, we will be making 4 passes. One pass per element, and as for the last element, it will be automatically sorted. Thus we can say that for an array of size n, n-1 passes are required to sort that array using the selection sort.



Top comments (0)