Welcome to part 4 of this series, where we will talk about automatic differentiation.
Github repo to code for this series:
 ashwins-code
/
Zen-Deep-Learning-Library
ashwins-code
/
Zen-Deep-Learning-Library
Deep Learning library written in Python. Contains code for my blog series on building a deep learning library.
Last post: https://dev.to/ashwinscode/deep-learning-library-from-scratch-3-more-optimisers-4l23
What is automatic differentiation?
Firstly, we need to recap on what a derivative is.
In simple terms, a derivative of a function with respect to a variable measures how much the result of the function would change with a change in the variable. It essentially measures how sensitive the function is to a change in that variable. This is an essential part of training neural networks.
So far in our library, we have been calculating derivatives of variables by hand. However, in practice, deep learning libraries rely on automatic differentiation.
Automatic differentiation is the process of accurately calculating derivates of any numerical function expressed as code.
In simpler terms, for any calculations we perform in our code, we should be able to calculate the derivates of any variables used in that calculation.
...
y = 2*x + 10
y.grad(x) #what is the gradient of x???
...
Forward-mode autodiff and reverse-mode autodiff
There are two popular methods of performing automatic differentiation: forward-mode and reverse-mode.
Forward-mode utilises dual numbers to compute derivatives.
A dual number is anything number in the form...
where is a really small number close to 0, such that
If we apply a function to a dual number as such...
you can see we calculate both the result of and the gradient of , given by the coefficient of .
Forward-mode is preferred when the input dimensions are smaller than the output dimensions of the function, however, in a deep learning setting, the input dimensions would be larger than that of the output. Reverse-mode is preferred for this situation.
In our library, we will implement reverse-mode differentiation for this reason.
Reverse-mode differentiation is a bit more difficult to implement.
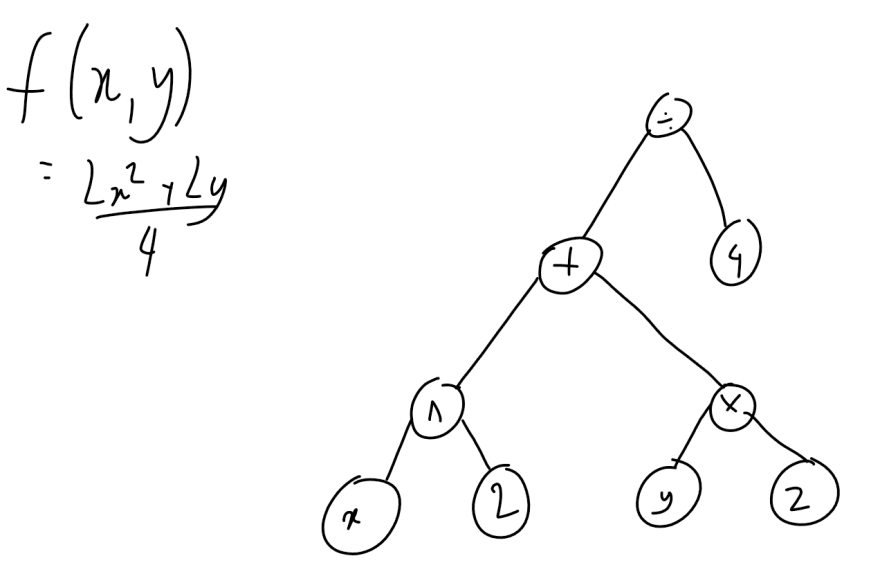
As calculations are performed, a computation graph is built.
For example, the following diagram shows the computation graph for
After this graph is built, the function is evaluated.
Using the function evaluation and the graph, derivatives of all variables used in the function can be calculated.
This is because each operator node would each come with a mechanism to calculate the partial derivatives of the nodes that it involves.
If we look at the bottom right node of the diagram (the node), the multiplier node should be able to calculate it's derivative with respect to the "y" node and the "2" node.
Each operator node would have different mechanisms, since the way a derivative is calculated depends on the operation involved.
When using the graph to calculate derivatives, I find it easier to traverse the graph in a depth-first manner. You start at the very top node and calculate it's derivative with respect to the next node (remember, you are traversing depth-first) and record that node's gradient. Move down to that node and repeat the process. Each time you move down a level in the graph, multiply the gradient you just calculated by the gradient you calculated in the previous level (this is due to the chain rule). Repeat until all the nodes' gradients have been recorded.
Note: it is not necessary to calculate all the gradients in the graph. If you want to find the gradient of a single variable, you can stop once it's gradient has been calculated. However, we'd usually want to find the gradients many variables, so calculating all the gradients in the graph all at once would be much computationally cheaper, since it would only require one graph evaluation. If you wanted to find the gradients of all the variables you wanted ONLY, you would have to do an evaluation of the graph for each variable, which would turn out to be much more computationally expensive to do.
Differentiation rules
Here are the different differentiation rules used by each node, which are used in calculating the derivates in the computation graph.
Note: all of these will show the partial derivative, meaning everything that is not the variable we are finding the gradient of is treated as a constant.
In the following, think of and as nodes in the graph and as the result of the operation applied between these nodes.
At multiplication nodes...
At division nodes...
At addition nodes...
At subtraction nodes...
At power nodes...
The chain rule is then used to backpropogate all the gradients in the graph...
However, when matrix multiplying, the chain rule get a bit different..
... where is a function that involves , meaning would be the gradient calculated in the previous layer of the graph. By default (aka if z is the highest node in the graph), , meaning would be a matrix of 1s with the same shape as .
The code
The Github repo I linked at the start contains all the code for the automatic differentiation part of the library and has updated all the neural network layers, optimisers and loss function to use automatic differentiation to calculate gradients.
To avoid this post being too long, I will show and explain the code in the next post!
Thank you for reading!



Top comments (0)