Ok, so let's quickly get this out of the way. If you want to implement a basic calculator in JavaScript that correctly handles +, -, *, and / operations, do the following (in order of preference):
- Don't, just use JavaScript, really, it does the job just fine!
const result = 2 + 2
// 4
- Use this one-liner (actually don't, this has a lot of potential issues!)
function calculate(expression) {
return eval(expression);
}
calculate("2+2") // returns 4
- Use a stack
- ... well, keep reading!
Problem statement
Let's first state the problem more clearly. Given a string which represents a mathematical expression with integers and 4 operations (+, -, *, and /), we want to evaluate that expression in the integer set and return its result. Note that the integer division (/) operation should truncate toward zero.
If this problem sounds familiar to you, you might have come across it on LeetCode (https://leetcode.com/problems/basic-calculator-ii/), or at least, I did!
Some examples of the expected behavior:
calculate("1") // 1
calculate("2+2") // 4
calculate("5+4*3") // 17
calculate("34/5+12*3/2-6+33/3+13") // 42
Compilers and Abstract Syntax Trees
So, the string representation of the mathematical expressions is great, but we can't really do much computation in that state. An arguably non-optimal idea would be to instead represent the expression in a tree. And so, the fun begins!
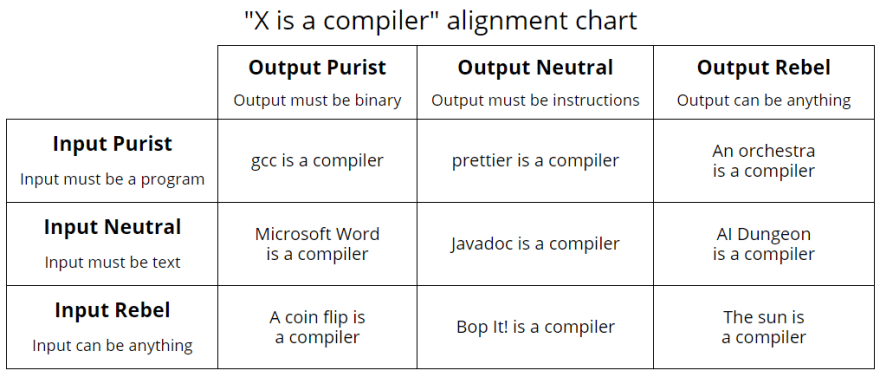
As a quick disclaimer, I acknowledge that it might be a stretch to title this section Compilers and Abstract Syntax Tree, but I guess we can agree that based on the following alignment chart, anything can be a compiler?
Alright, so first, let's look at what tree representation we are aiming for based on the previous four example string inputs.
Now let's look step by step at how we can build such trees from their corresponding string representations.
The first thing we notice, is that each node of the tree holds either an integer value or an operation. Each node also has up to 2 children, one on the left and one on the right. We also keep track of the parent node to facilitate certain cases when constructing the tree from the string representation. As such, we can represent each node as an object with the structure:
type Node = {
value: number;
operation: string;
left: Node;
right: Node;
parent: Node;
}
Note that we are using TypeScript here just for illustration purposes, as the code presented hereafter is in JavaScript.
Each node can either have a value or an operation. There are probably better ways of representing a node, but this will do just fine!
We initialize the tree with an empty root node and a pointer on that node:
let root = {};
let currentNode = root;
Now, let's start with the easiest part, which is to recognize integers from the string representation.
for (let i = 0, length = s.length; i < length; i++) {
let char = s.charAt(i);
if (/[0-9]/.test(char)) {
let number = char;
while (/[0-9]/.test(s[i + 1])) {
char = s[i + 1];
number += char;
i = i + 1;
}
if (currentNode.left == null) {
currentNode.left = { value: parseInt(number, 10) };
} else if (currentNode.right == null) {
currentNode.right = { value: parseInt(number, 10) };
}
}
// We'll look at this later!
if (["+", "-", "*", "/"].includes(char)) {
...
}
}
Here we are checking if the upcoming character in the string is a digit. As it can be the first of a multiple digit number, we go on an internal while loop and concatenate all subsequent digits. Finally, we create a new node and put the value in on either the left or the right of the current node depending on which is empty.
We can reuse the same loop to parse operations as well:
for (let i = 0, length = s.length; i < length; i++) {
let char = s.charAt(i);
if (/[0-9]/.test(char)) {
...
}
if (["+", "-", "*", "/"].includes(char)) {
if (currentNode.operation == null) {
currentNode.operation = char;
} else {
const newNode = { operation: char };
if (
["+", "-"].includes(currentNode.operation) &&
["*", "/"].includes(newNode.operation)
) {
newNode.left = { ...currentNode.right };
currentNode.right = newNode;
newNode.parent = currentNode;
} else if (
["*", "/"].includes(currentNode.operation) &&
["*", "/"].includes(newNode.operation)
) {
if (!currentNode.parent) {
newNode.left = currentNode;
currentNode.parent = newNode;
root = newNode;
} else {
currentNode.parent.right = newNode;
newNode.parent = currentNode.parent;
newNode.left = currentNode;
}
} else {
newNode.left = root;
root.parent = newNode;
root = newNode;
}
currentNode = newNode;
}
}
}
Ok, so there is quite a lot happening here.
Let's first look at the first case, where the current node doesn't have an operation. In that case, we simply set the current node's operation to the character value we are processing.
Next, we create a node, with the current char as the operation value. We then have a few more distinct cases.
Because we need to adhere to the basic rules of arithmetic, * and / take priority over + and -. In terms of constructing our tree, that means that the new node will be a child of our current node and that the node at the right of our current node needs to become the new node's left child.
Another particular case is when we have successive * and / operations. If the current node we are processing is the root, we can make the new node the root, as the order of those operations doesn't matter. If the current node is not the root, we need to locally do the same operation, hence the need to keep track of parent nodes as well!
To finish the construction of the tree, we need to deal with the case where we have successive + and - operations. This case is similar to the previous when it happens at the root, but because of the rules of arithmetic, here we always update the root node, as the current node will always be at the root.
Finally, we compute and return the result of the computation:
/**
* @param {string} s
* @return {number}
*/
function calculate(s) {
let root = {};
let currentNode = root;
for (let i = 0, length = s.length; i < length; i++) {
let char = s.charAt(i);
if (/[0-9]/.test(char)) {
...
}
if (["+", "-", "*", "/"].includes(char)) {
...
}
}
if (!root.operation) {
return root.left.value;
}
return compute(root);
}
Note that we need to add a special case for strings containing only a number (e.g. "1"). In such cases, the root node won't have any set operation, so we just return the value stored in its left child node.
More on this compute() function in the next section!
Computing
Now, for the easier part of this pointless exercise: the computation!
Once we have (correctly) built a syntax tree from the string expression, we recursively compute each node in a depth-first manner and we return the final result.
The order of computation that we are looking for is bottom-up, meaning that we first compute the leaves and gradually move up the tree by replacing operation nodes with the result of their operation on their left and right sub-trees.
From that, we deduce that a depth-first traversal would do the trick:
function compute(root) {
if (root.value != null) {
return root.value;
}
if (root.operation) {
let left = compute(root.left);
let right = compute(root.right);
switch (root.operation) {
case "+":
return left + right;
case "-":
return left - right;
case "*":
return left * right;
case "/":
return Math.floor(left / right);
}
}
}
Congratulations, you've survived this ridiculous exercise! Hopefully it was either entertaining, or valuable, or both. As stated in the introduction of this post, this is neither the easiest implementation nor the most optimal. Friendly advice: if you are looking at cracking this problem on LeetCode, use a stack!
That's all folks!













Top comments (0)