Validate a Binary Search Tree

Question: Given a binary tree, determine if it is a valid binary search tree (BST).

Pretty simple right? Let's recap what a binary search tree is.
For a given node, the left subtree of the node contains the value less than current node and the right subtree of the node contains a value greater than the current node. Such tree's called binary search trees.

Eg :

So the left node value should be less than the parent node and the right node value should be greater than the parent node value.

ie two conditions,

function TreeNode(val) {
     this.val = val;
     this.left = this.right = null;
}

var dfs = function(root){
       if(root == null) return true;
       if(root.left.val < root.val && root.right.val>root.val)
           return dfs(root.left) && dfs(root.right);
       else
           return false;
}

is that it?
Well no. Here we need to emphasize the keyword "subtree". So all the node of left subtrees to the current node must have value less than the current node and all the node of right subtree to the current node must have value greater than the current node.
Eg: consider the tree

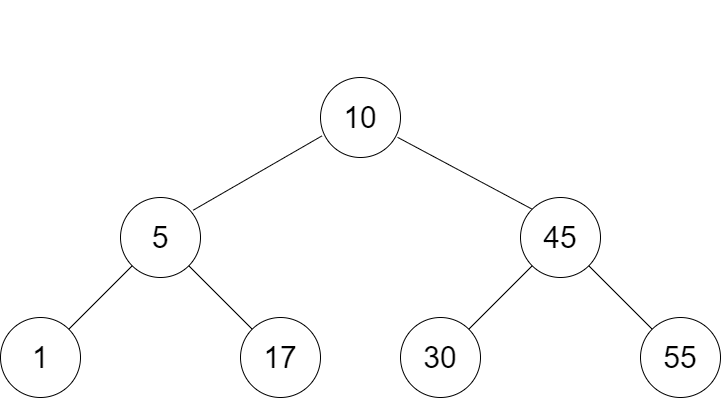
will it pass the above code? yes, is it valid? no, since even though for subtree with root 5 follows the rule of BST, but for root value 10, it breaks the BST since 17>10, it cannot lie in the left subtree.

So we need a way to communicate that, if I am traversing towards the left of the current root, then the current node value is the maximum value I am allowed to see, similarly, if I am traversing towards right then current node value is the minimum value I am allowed to see.

Since for traversing a tree we follow recursion, let's write our recurisve function.

1> dfs(root,min,max)
here I named my function dfs, I am calling it with a root and two addition parameters, min and max which specify the minimum and maximum value I am allowed to see for the subtree. Since when starting out from root, it doesnt have a min or max values we initialize it as null.

var isValidBST = function(root){
      dfs(root,null,null);
}

dfs(root.left,min,root.val)
// this statement means when I go towards left, 
// the min will remain min and max value is parent root value.

dfs(root.right,root.val,max)
// this statement means when I go towards right, 
// the max will remain max and min value is parent root value.

when we call this function for the first time, the min and max values will be null, now when this function is again called recursively the min and max values wont remain null, so we need to perform checks in those conditions.

if((min != null && root.val<=min) || (max != null && root.val>=max)) return false;

This means when we have a minimum value and the current root value is less than the minimum possible value that's false, also if max is not null and current root value is greater than max possible value, that's false.

The beauty of this statement lies within the fact that when we recurse to far left, the minimum remains null and we care only about maximum, similar when we recurse towards far-right.

var isValidBST = function(root) {
    if (!root) {
        return true; // Sanity check for passing test case '[]'
    }

    function helper(root, min, max) {
        if (!root) {
            return true; // We hit the end of the path
        }

        if ((min !== null && root.val <= min) || (max !== null && root.val >= max)) {
            return false; // current node's val doesn't satisfy the BST rules
        }

        // Continue to scan left and right
        return helper(root.left, min, root.val) && helper(root.right, root.val, max);
    }

    return helper(root, null, null);
};

github: https://github.com/AKHILP96/Data-Structures-and-Algorithms/blob/master/problems/ValidateBST