Question: You're given a sorted array but it's rotated around a pivot. You're given a target value to search. If found return the index or return -1. Assume that array doesn't contain duplicates.
Eg:
sorted array = [0,1,2,4,5,6,7]
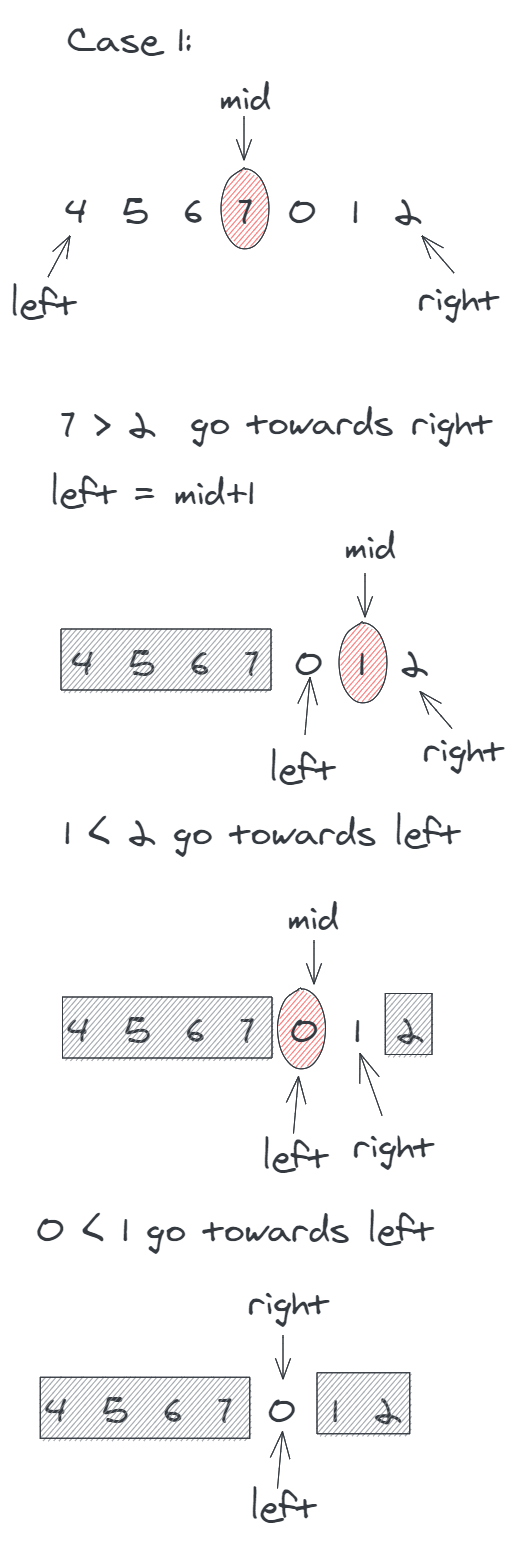
rotated array = [4,5,6,7,0,1,2]
If the target is 5, we return 1.
Brute Force : O(n)
Brute Force approach would be to traverse through the array and return the index. Plain and simple.
But as you know brute force search on a sorted list is not the best idea :

Binary Search : O(log n)
A little demo on how Binary Search works :

We want to modify the binary search algorithm since the given array is rotated at a pivot and is not strictly sorted.
Let's start with what we have and know how to work on it.
Since the array is Rotated Sorted array, and we know how to perform binary search on a sorted array. SO let's divide the array into two halves and call the left and right.
Once we get the two sorted arrays, we can perform a binary search on the two sorted arrays and get find the target in O(long). Pretty cool right?
BUT how to find the pivot point where we should divide the array?
One way is to search for the pivot by going through the list but it would take O(n) time. So we need a different way of searching for that pivot.
How about using Binary Search for Pivot?
You might now be thinking, "Akhil, you just said that we can't perform Binary Search to find the target but you're using Binary Search for finding the pivot ?? Isn't pivot similar to target?"
Yes, you're right but notice that while searching for target, we're literally blind, but while searching for pivot, we know for a fact that arr[pivot-1] > arr[pivot] < arr[pivot+1] , and we're going to use this one key property to find that sweet little pivot.
Here we're just converting towards finding that minimum element in the array.
We face 2 cases :
1> if arr[mid] > arr[right], it means we're in right sorted array, so go towards left to find the pivot element.
2> else it means the array is rotated, so go towards left to find that right sorted array.
Let's code it :
let left = 0;
let right = nums.length-1;
while(left < right){
let mid = Math.floor((left+right)/2);
if(nums[mid]>nums[right]){
left = mid+1;
}else{
right = mid;
}
}
Now that we've found our pivot, let's work on finding the target.
So, how to figure out where is our target located, is it in the left subarray or right subarray ?
Let's code this part:
let pivot = left;
left = 0;
right = nums.length-1;
if(nums[pivot]<=target && target <= nums[right]){
left = pivot;
}else{
right = pivot;
}
Now that we know which part our target lies, let's perform binary search on that subarray:
while(left<=right){
let mid = Math.floor((left+right)/2);
if(nums[mid] == target){
return mid;
}
if(nums[mid]<target){
left = mid+1;
}else{
right = mid-1;
}
}
return -1;
Now that we have all the bit's and parts, lets put it all together :
var search = function(nums, target) {
if(nums.length == 0 || nums == null) return -1;
let left = 0;
let right = nums.length-1;
while(left < right){
let mid = Math.floor((left+right)/2);
if(nums[mid]>nums[right]){
left = mid+1;
}else{
right = mid;
}
}
let pivot = left;
left = 0;
right = nums.length-1;
if(nums[pivot]<=target && target <= nums[right]){
left = pivot;
}else{
right = pivot;
}
while(left<=right){
let mid = Math.floor((left+right)/2);
//console.log(mid , nums[mid] , target);
if(nums[mid] == target){
return mid;
}
if(nums[mid]<target){
left = mid+1;
}else{
right = mid-1;
}
}
return -1;
};
That's it ! Now you know how to apply and take advantage of binary search in weird conditions.
Thank's a lot if you've made it till here 🥰, leave comment's down below if you've any doubts or you want me to cover a question.





Top comments (2)
Can you write on Advanced Binary Search and it's applications in different problems like finding the rotation count(pivot) in rotated sorted array or find pairs whose sum is already present in given array. BTW nice article. Thnx :)
Thanks for your inputs !! Rotation count is the first part of this problem, finding that pivot.
And I have written about find pairs whose sum exists in the array here :
dev.to/akhilpokle/2-ways-to-two-su...
If you have any interesting questions on your mind, please let me know : )