Minimum Number of Arrows to Burst Balloons

Question: There are a number of spherical balloons spread in two-dimensional space. For each balloon, provided input is the start and end coordinates of the horizontal diameter. your task is to burst all the balloons with a minimum number of arrows.
Eg: let suppose given array is the horizontal diameter of ballons : [[1,3],[2,7],[5,9],[2,9],[9,12],[8,10],[12,15],[11,13]] and your task is to find minimum number of arrows to burst all balloons.

Let's break it down.
1> Balloons can be seen as x-coordinates start and end points.
2> We're aiming for bursting as many balloons as possible in a single arrow.
3> This leads us to find all the balloons whose x-coordinates overlap so that we can cover maximum possible balloons.
4> Also note that inputs are not strictly increasing/decreasing start and end points, will sorting help us?

Let's visualize it.

This is how balloons stack up.

From the above observation we can say that we're greedily choosing ballons that have common start and end point range.

Step 1:
Since we're finding common start and end points, random start and end points won't help so let's sort the array.
balloons : [[1,3],[2,7],[2,9],[5,9],[8,10],[9,12],[11,13],[12,15]]

Step 2:
We need a start and end points of the first balloon as the initial point.
end = balloon[0][1] //
count =1 // need at least one arrow to burst one balloon

Step 3:
Now how to proceed further? Lets go to back to our basic requirement, burst as many balloons as possible with one arrow. So we've to find all the balloons whose start and end diameters lie between the current start and end diameters.

balloon 1: 
start = 1 
end = 3

balloon 2: // within range
start = 2
end = 7

balloon 3: // within range
start = 2
end = 9

balloon 4: // out of range 
start = 5
start = 9

let burst first three balloons with one arrow

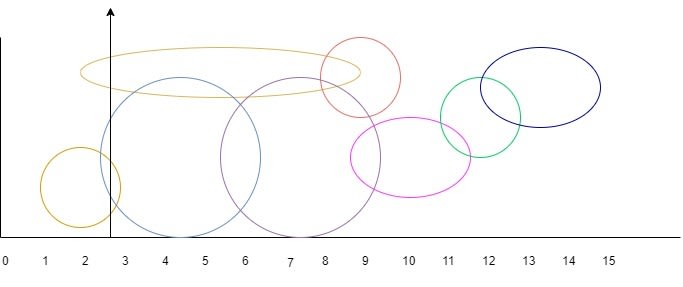
Arrow 1

Since balloon 4 was out of the range of the previous arrow, we need one more arrow to shoot down balloon 4, but at the same time we have to burst as many balloons as possible with it.

These observations will help us derive to our solution.

let's write some code :

First arrow :

Arrow 1 start = 1, end = 3 burst balloons [1,3],[2,7],[2,9]

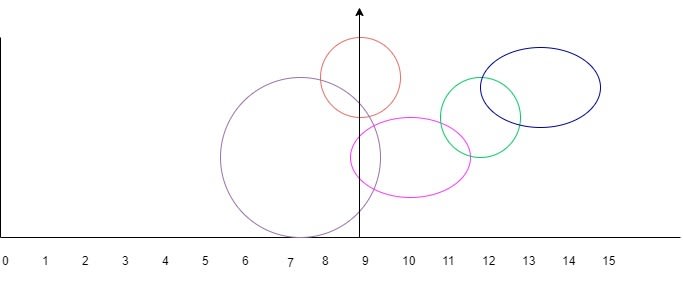
Arrow 2 start = 5 end = 9 burst balloons [5,9],[8,10],[9,12]

Arrow 3 start = 11 end = 13 burst balloons [11,13],[12,15]

Now you know how to burst balloons

github : https://github.com/AKHILP96/Data-Structures-and-Algorithms/blob/master/problems/burstBalloons.js