Question: Given an array, find the maximum subarray sum.
Eg: For given array : [-2,1,-3,4,-1,2,1,-5,4]
output : 6 for subarray [4,-1,2,1]
Brute force: O(n^2)
Brute force solution would be to go generate all possible subarray and find the maximum subarray.
var maxSubArray = function(nums) {
if(nums.length == 0) return 0;
let max = nums[0];
for(let i=0;i<nums.length;i++){
let sum = 0;
for(let j=i;j<nums.length;j++){
sum+=nums[j];
if(max<sum) max = sum;
}
}
return max;
};
Now let's observe and find patterns that might help us optimize our solution.
For an Array A let's consider the following observations
If for subarray Sum(A[i,....,j-1]) < A[j], then we know that there's no need to calculate Sum(A[i+1....,j-1]) again since it will definitely be less than A[i].
So based on this, if we come across a situation where current element is greater than sum of previous elements, then we shall start a new subarray from the current subarray.
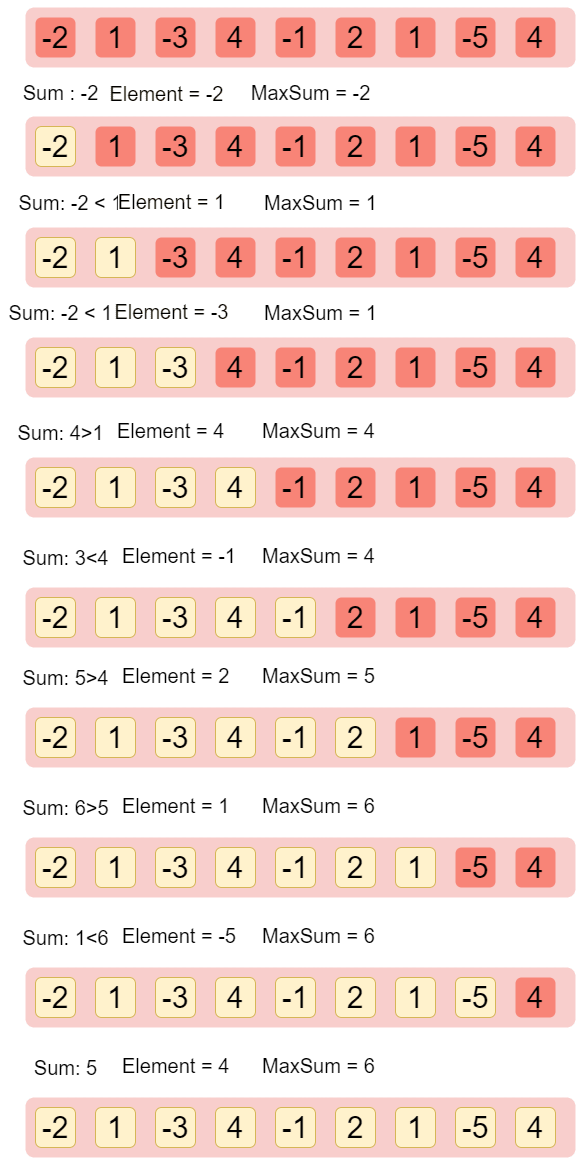
Let's understand this :
So as you can see here,
1 > we maintain two containers, sum and maxSum, we keep on adding elements to sum and compare it with maxSum, and change maxSum only if sum>maxSum.
2 > we change sum when the current element is greater than sum.
this approach improve our time from O(n^2) to O(n).
code:
var maxSubArray = function(A) {
let sum = A[0];
let maxSum = A[0];
for(let i=1;i<A.length;i++){
sum = Math.max(sum+A[i],A[i]);
maxSum = Math.max(maxSum,sum);
}
return maxSum;
};
github : https://github.com/AKHILP96/Data-Structures-and-Algorithms/tree/master/problems


Top comments (0)