Question: Give a number N, count the total number of prime numbers between 0 and n.
What's a prime number ? A prime number is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.
Brute Force:
So, for a given number n, a natural way would be to go through each number and verify if there are any numbers between 1 and n-1 for which n%x == 0 ie for a number x, the remainder is 0.
var countPrimes = function(n) {
if(n === 1){
return 0;
}
let count = 0;
for(let i = 2; i < n; i++){
if(i !== 2 && i % 2 == 0){
continue;
}
if(isPrime(i)){
count++;
}
}
return count;
};
function isPrime(num) {
var sqrtnum=Math.floor(Math.sqrt(num));
var prime = num != 1;
for(var i=2; i<sqrtnum+1; i++) {
if(num % i == 0) {
prime = false;
break;
}
}
return prime;
}
It works in O(n^2), since for each number, we check if any number between 0 to n-1 is divisible by n.
Can we do better? Yes we can. Here I want you to observe that each time when we check if a number is prime or not, we're performing a lot of repeated tasks, so instead of checking if x is prime or not from 0 to x-1, how about we make an array and set the multiples of x as composite.
Here, ask you're interviewer, what's the range of n
(*tip interviewer will like you if you ask questions, unlike your crush who's annoyed when you ask questions)
so if the given n = 100. Create an array of size 100 and initialize it to false.
let prime = new Array(101);
Now set all the entries to false. Why ? just stay with me.
arr.fill(prime);
Now start looping from 2 and set all multiples of 2 to true. Repeat the same whenever you come across an array element set to false.
let res = 0;
for (let i = 2; i < n; i++) {
if (notPrimes[i] === false) {
res++;
for (let j = 2; i * j < n; j++) {
notPrimes[i * j] = true;
}
}
}
What we're doing here is whenever we come across an array element for which it's set to false, it means that particular number "i", isn't multiple of anything before it so we'll increment the count and set all the multiples of "i" to true, ie we've seen multiple of that number.
If you want to increase its speed even further, you can modify the inner for loop as :
for (let j = i*i; i * j < n; j++) {
notPrimes[i * j] = true;
}
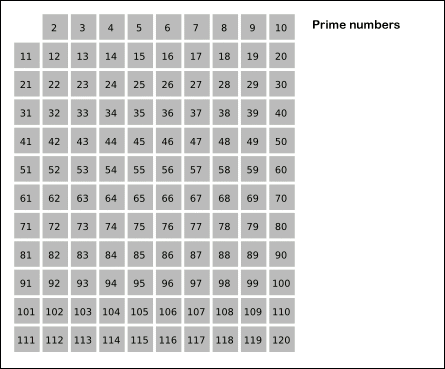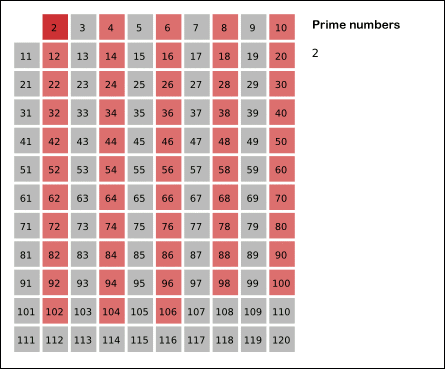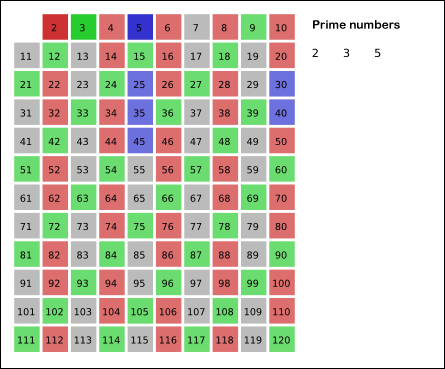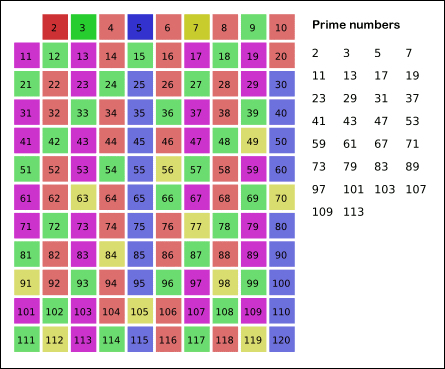
This is because let's consider 2, when we go over 2, we set 4,6,8,10.. to true, so when we come across 3, we're wasting time computing 3*2, we know that 3*2 would be set, so let's start from 3*3 = 9, similar for 5, in case of 5, multiples of 5 ie 10,15,20 would be already set by 2 & 3 so start from 25.
This approach takes O(n) time since we're visiting each number once, and O(n) space.
Now you know how to find prime numbers at blazing fast speed.
github : https://github.com/AKHILP96/Data-Structures-and-Algorithms/blob/master/problems/countPrimes.js


Top comments (0)