Hello there,
This is my first post on this site. I've been running a Turkish/English blog on Medium platform for 28 months now and have just discovered this site. I absolutely fell in love with its retroesque design, so here we are. As you can see, I am looking forward for job opportunities abroad. Feel free to contact me for any vacancies.
Methodology
Runs test is a hypothesis testing based methodology that is widely used in statistical analysis to test if a set of values are generated randomly or not. It is a hypothesis test so we have a pair of a null hypothesis and an alternative one.
Null hypothesis: The values are randomly generated.
Alternative hypothesis: The values are NOT randomly generated.
A Z score for hypothesis can be acquired by simply following the general formula:
(Observed-Excepted) / Standard Deviation
The score is then tested against the confidence interval(two-tailed) we specify. If the value is higher, we conclude that our alternative hypothesis holds. Otherwise, if the value is lower, we cannot say anything about the randomness of data at this significance level. We will be using %95 confidence interval(alpha = 0.05) through the rest of this article.
Definitions and Formulas
- A run: A series of positive or negative values:
Data: [1, -2, -3, 4, 5, 6, –7]
Runs: [[1], [-2, -3], [4, 5, 6], [-7]]
- Score Formula
(Number of runs - Excepted Value for Number of Runs) / Standard Deviation
- Expected Value Formula for Runs Test
n_p = Number of positive values
n_n = Number of negative values
Excepted value of runs = (2 * n_p * n_n) / (n_p + n_n) + 1
- Standard Deviation Formula for Runs Test
n_p = Number of positive values
n_n = Number of negative values
Excepted value of runs = (2 * n_p * n_n) / (n_p + n_n) + 1
Test Data
I will using the data provided by NIST.
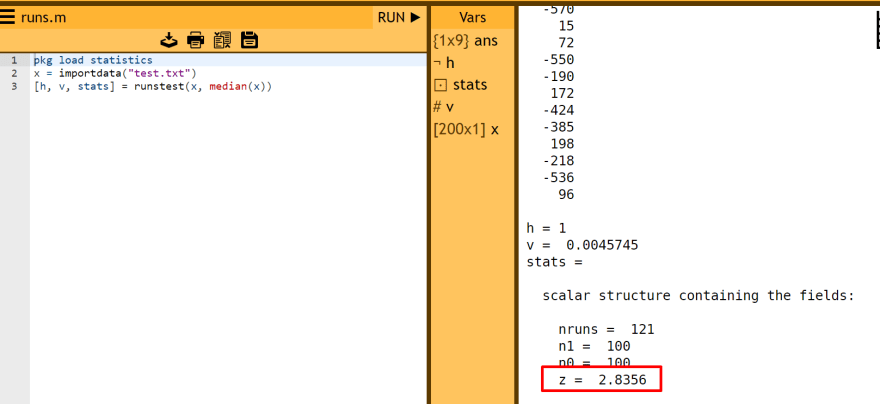
Octave/Matlab Implementation and Results
Using online Octave:
- Upload text file
-
Load ‘statistics’ package
pkg load statistics
-
Import data to array
x = importdata("test.txt")
-
Run runstest
[h, v, stats] = runstest(x, median(x))
Python Implementation
Implement the test using Python.
Running the code produces the results below (Calculated Z Score, Z Score at %95 confidence):
(2.8355606218883844, 1.6448536269514722)
Since our test score is higher, alternative hypothesis holds. This means that our values are genuinely random.
Thanks for reading. Any corrections are welcome.



Top comments (0)