Binary Tree – How to implement using Javascript in 2022?

In this article, we will read about the binary tree in detail. We will see how to build and traverse it in javascript.

Tree data structure

A tree is a non-linear data structure that follows some hierarchy. It is a collection of the tree nodes.

A tree node stores the information about its node value, its left child address, and right child address.

In a tree, a tree node can have multiple children.

Basic Terminology in Tree

Before diving into the code, let’s understand the basic terminologies –

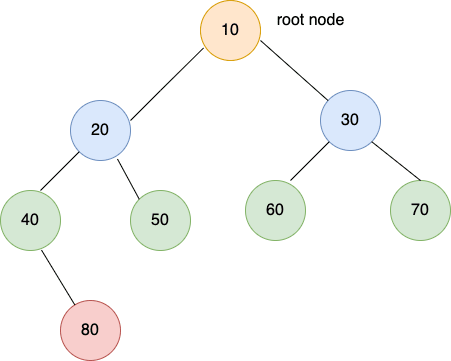
root – root is the topmost node of the tree e.g 10 is the root node in the above picture.

siblings – The children of the parent are siblings to each other e.g 20 & 30 are siblings as both are children of node 10.

cousins – uncles’ children are cousins to ourselves e.g node 30 is the uncle of nodes 40 & 50. Hence, nodes 40, 50, 60, and 70 are all cousins.

height of a node – Distance from the current node to the farthest leaf e.g Height(20) = 2 because 80 is the farthest leaf from node 20.

depth of a node – distance from the root to the node e.g depth(20) = 1

Height of entire tree = Height of the root node

Depth of entire tree = Height of entire tree

Binary Tree data structure

A binary tree is a tree where a tree node can have 0, 1, or 2 children at most.

How to Implement binary tree in Javascript?

function TreeNode(data) {
  this.data = data;
  this.left = null;
  this.right = null;
}

function createTree() {
  let root = new TreeNode(10);

  root.left = new TreeNode(20);
  root.right = new TreeNode(30);

  root.left.left = new TreeNode(40);
  root.left.right = new TreeNode(50);

  root.right.left = new TreeNode(60);
  root.right.right = new TreeNode(70);

  root.left.left.right = new TreeNode(80);

  return root;
}

How to traverse a binary tree?

Traversal means visiting each node of the binary tree.

There are 3 ways to traverse a binary tree –

1. Preorder traversal
2. Inorder traversal
3. Postorder traversal

There is one more traversal Level Order traversal that is not in the scope of this article. We will read that when we solve the Left View, Right View of the binary tree, etc.

Preorder Traversal (using recursion)

It traverses the tree in the following fashion – data Left Right.

The preorder traversal for the above tree is – 10 20 40 80 50 30 60 70

function preOrder(root) {
  if (root === null) return;

  // print the node data
  console.log(root.data);

  // goto left
  preOrder(root.left);

  // goto right
  preOrder(root.right);
}

Time Complexity: O(n) (each tree node is processed once)

Space Complexity: O(h) h is the height. of the tree.

Preorder Traversal (without recursion)

The recursive one was pretty simple but if you’re going to apply for a software developer position you might be asked to traverse the tree iteratively i.e without recursion.

We would be using one stack to remember the previous node and one array to store the answer.

To solve this, think of the preorder formula – data left right and visualize it.

Consider an example with just 3 nodes –

       5

   /       \
 10        15

Preorder for this is – 5 10 15

Now, after processing node 5, next will be node 10. If we are using a stack and pushing the left and right node of the current node, then the right node will be pushed first and then the left one because we need to traverse left children first.

If you understood this, the implementation will be easier to understand.

function preOrder(root) {

  let ans = [];

  if (root === null) return ans;

  // push root into stack
  let stack = [root];

  // loop while stack is not empty
  while (stack.length) {

    let cur = stack.pop();

    // push the node data to ans
    ans.push(cur.data);

    // push right node into stack
    if (cur.right) {
      stack.push(cur.right);
    }

    // push left node into stack
    // as it pushed last so will be pop first
    // i.e this ensures data left right ordering
    if (cur.left) {
      stack.push(cur.left);
    }

  }

  return ans;
}

Time Complexity: O(n) (each tree node is processed once)

Space Complexity: O(h) + O(n) ~= O(n) h is the height of the tree.

Inorder Traversal (using recursion)

It traverses the tree in the following fashion – Left data Right

The inorder traversal for the above tree is – 40 80 20 50 10 60 30 70

function inOrder(root) {
  if (root === null) return;

  // goto left
  inOrder(root.left);

  // print the node data
  console.log(root.data);

  // goto right
  inOrder(root.right);
}

Time Complexity: O(n) (each tree node is processed once)

Space Complexity: O(h) h is the height. of the tree.

Inorder Traversal (without recursion)

Inorder formula: left data right

From the formula, we will follow below steps —

Step1: We will go to the left and keep pushing every node into the stack.

Step2: Pop the stack top element

Step3: goto right and follow Step1

function inOrder(root) {

  let ans = [];

  if (root === null) return ans;

  // push root into stack
  let stack = [];

  let cur = root;

  // loop while stack is not empty
  while (cur || stack.length) {

    // goto left
    while(cur) {
      stack.push(cur);
      cur = cur.left;
    }

    // push the node data to ans
    cur = stack.pop();
    ans.push(cur.data);

    // push right node into stack
    cur = cur.right;

  }

  return ans.reverse();
}

Time Complexity: O(n) (each tree node is processed once)

Space Complexity: O(h) + O(n) ~= O(n) h is the height of the tree.

Postorder Traversal (using recursion)

It traverses the tree in the following fashion – Left Right data

The postorder traversal for the above tree is – 80 40 50 20 60 70 30 10

function postOrder(root) {
  if (root === null) return;

  // goto left
  postOrder(root.left);

  // goto right
  postOrder(root.right);

  // print the node data
  console.log(root.data);
}

Time Complexity: O(n) (each tree node is processed once)

Space Complexity: O(h) h is the height. of the tree.

Postorder Traversal (without recursion)

Let’s think of the preorder traversal solution again. This is similar to that.

preorder formula: data left right

Let's see how can we reach to postorder from the preorder.

Now, reverse the left and right position, the formula will become data right left

And if we reverse the entire formula, the final formula will become – left right data

which is the formula for the postorder traversal.

function postOrder(root) {

  let ans = [];

  if (root === null) return ans;

  // push root into stack
  let stack = [root];

  // loop while stack is not empty
  while (stack.length) {

    let cur = stack.pop();

    // push the node data to ans
    ans.push(cur.data);

    // push left node into stack
    if (cur.left) {
      stack.push(cur.left);
    }

    // push right node into stack
    if (cur.right) {
      stack.push(cur.right);
    }
  }

  return ans.reverse();
}

Time Complexity: O(n) (each tree node is processed once)

Space Complexity: O(h) + O(n) ~= O(n) h is the height of the tree.

Conclusion

We have seen the implementation of the binary tree in javascript and its traversal preorder, inorder, and postorder in both recursive and non-recursive ways.

The idea of this article is to give you consolidated knowledge all at once. From the interview point of view, the non-recursive traversals are very important.

If you like my article, please buy me a coffee!

I'm also on medium, please follow me there.

Thanks for reading the article!