Behold, the degree sum formula:
The degree sum formula states that, given a graph G = (V,E), the sum of the degrees is twice the number of edges. Let's look at K3, a complete graph (with all possible edges) with 3 vertices.
First, recall that degree means the number of edges that are incident to a vertex. A vertex is incident to an edge if the vertex is one of the two vertices the edge connects. In the case of K3, each vertex has two edges incident to it. Actually, for all K graphs (complete graphs), each vertex has n-1 degrees, n being the number of vertices. Dope.
So, for each vertex in the set V, we increment our sum by the number of edges incident to that vertex. Or, in another way, construct a degree sequence for a graph and sum it: sum([2, 2, 2]) # 6. This sum is twice the number of edges. Our graph should have 6 / 2 edges.
The "twice the number of edges" bit may seem arbitrary. But each edge has two vertices incident to it. In the degree sum formula, we are summing the degree, the number of edges incident to each vertex. A degree is a property involving edges. Edges are connections between two vertices. Summing the degrees of each vertex will inevitably re-count edges.
Properties we can derive from this formula
Anything multiplied by 2 is even. Since the sum of degrees is two times the number of edges the result must be even and the number of edges must be even too.
With the above knowledge, we can know if the description of a graph is possible. This is useful in a puzzle such as the one I found in this book:
At a recent math seminar, 9 mathematicians greeted each other by shaking hands. Is it possible that each mathematician shook hands with exactly 7 people at the seminar?
Each mathematician would shake the hand of 7 others which amounts to shaking hands with every mathematician minus yourself and one other person.
A graph may not have jumped out at you, but this puzzle can be solved nicely with one. Think of each mathematician as a vertex and a handshake as an edge.
Can we have a graph with 9 vertices and 7 edges? Applying the degree sum formula, we can say no.
When we sum the degrees of all 9 vertices we get 63, since 9 * 7 = 63. Since the sum of degrees is twice the number of edges, we know that there will be 63 ÷ 2 edges or 31.5 edges. Since half a handshake is merely an awkward moment, we know this graph is impossible.
I hate telling mathematicians that they can't shake hands. Can we have 9 mathematicians shake hands with 8 other mathematicians instead?
Can we have a graph with 9 vertices and 8 edges?
Summing 8 degrees 9 times results in 72, meaning there are 36 edges.

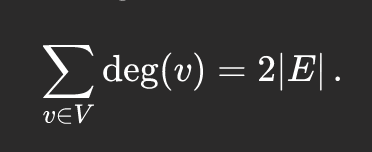


Top comments (0)