Time Complexity. The Low Down

If you have spent any time in a coding community you have probably heard the term Big O and/or time complexity. Not knowing, at least, what these terms mean can instill feelings of imposter syndrome or incompetence. In this article I am going to introduce time complexity and how to calculate the Big O of a function. While these calculations are trivial to some degree, knowing the concept and how it works can be very beneficial. Let’s begin.

What is the point?

Time complexity is used to calculate the amount of time it takes a function to complete. Let’s use a simple “sum of all numbers” function as an example. A user passes in a number, starting from 1, we add all numbers until we reach the number passed in. For instance:
addUpTo(5)
would return
1+2+3+4+5 = 15.
There are tons of ways we could define this function, however some are faster than others. By calculating the Big O of our function definition we are able to compare the time complexity of two algorithms thus revealing which is faster.

What is Big O notation?

Common outcomes for Big O in succession are

O(1)
O(log(n))
O(n)
O(nlog(n))
O(n^2)

reference: https://cooervo.github.io/Algorithms-DataStructures-BigONotation/

the fastest being O(1) (constant run time) and the longest being O(n^2). In this article we will only be covering

O(1)
O(n)
O(n^2)

as they are simpler to grasp. These notations represent the speed at which a function may run as the passed in input is increased. Let's use addUpTo(n) as an example. As n becomes larger this function may or may not take longer to compute depending on what its time complexity is. If the Big O of our algorithm turns out to be O(n) then the runtime increases as n does in a linear fashion. For instance addUpTo(100000) will take much longer to run than addUpTo(5). However, if our Big O = O(1) then it is considered to be a “constant runtime” which is not affected by the size of n.

How do we calculate it?

We can calculate the Big O of an algorithm by counting the number of simple instructions it uses. Let's use these two different algorithms for our addUpTo(n) function:

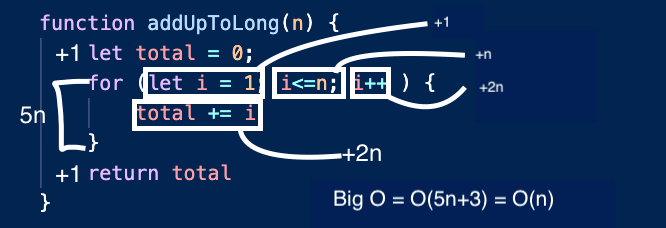
function addUpToLong(n) {
    let total = 0;
    for (let i = 1; i<=n; i++ ) {
        total += i
    }
    return total
}

function addUpToShort(n) {
    return n * (n + 1) / 2
}

Both of these algorithms output the same result however, notice I have named one long and one short. That is because the Long function has a longer runtime than Short does. Lets add up all of the simple instructions for the Long function first:

Initializations, operations, comparisons, and returns are all constant run time so O(1). In this case all of the constant expressions are:
let total = 0
let i = 1
return total

So currently we have 3 constants which means Big O thus far = O(3)

Anytime there is a loops that iterates through a list or increments from 0 to n we consider this O(n) runtime. This means that as the number or list gets larger, the time that the algorithm takes to complete increases simultaneously. In this case the runtime is dependent on n. In our example here we have a for loop so every simple expression that would usually be constant will re-occur n times with the exception of the initial let i = 1 since that only runs once regardless of how many times we loop. All of the O(n) expressions are:
i<=n
i++
total += 1

i++ and total += 1 both count as two expressions since we are doing two operations at once. An initialization and an increment. The Big O calculations for this algorithm are thus as followed:

Is it necessary to count instructions?

The simple answer here is no actually and thank goodness for that! How tedious it would be to count all the expressions of our all of our algorithms. The proper way to calculate Big O and time complexity is actually to recognize overall trends rather than specific number of instructions.

As n reaches infinity small things like constants become unimportant. For instance if we invoke addUpToLong(9999999) that +3 and even the 5 in 5n doesn’t really matter as it does not change the overall trend which will still always be linear. Therefore, we can simplify O(5n+3) down to just O(n). in addUpToShort the O(3) simplifies to O(1) as it will always be constant. Most importantly, this means we do not have to do trivial calculations like I showed in the example. We can simply just recognize how our algorithms are running based off of a simple glance.

If there is no looping dependent on n then the run time is O(1) if there is a single loop that is dependent on n then runtime is O(n) and if there is a nested loop that is dependent on n then the runtime is O(n^2). An O(n^2) could look like the following:

function printAllPairs(n) {
    for(let i = 0; i < n; i++){
        for(let j = 0; j < n; j++){
            console.log(i, j)
        }
    }
}

How is this useful?

Being able to quickly identify an algorithm's time complexity can be extremely beneficial if you are working with massive databases. In my examples it may seem trivial. Who cares if a function takes a second to run rather than .25 seconds right? Well what If we are writing an algorithm where n is equal to numbers in the millions coming from a massive database? Those runtimes start to look like minutes and maybe even hours to run. Learning to maximize efficiency in big data projects becomes a life saver in some cases.

Thank you for reading my blog. I hope these examples proved to be useful and coherent for you! If you would like to pull my repo with these functions and see their runtimes then feel free to clone my repo and run it: https://github.com/Aaidenplays/data-structures-and-algorithms-2