Problem statement
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted from left to right.
- The first integer of each row is greater than the last integer of the previous row.
Problem statement taken from: https://leetcode.com/problems/search-a-2d-matrix
Example 1:
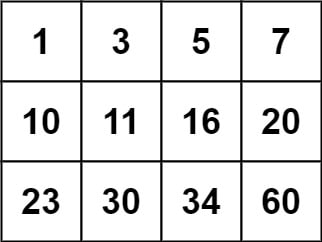
Input: matrix = [[1, 3, 5, 7], [10, 11, 16, 20], [23, 30, 34, 60]], target = 3
Output: true
Example 2:
Input: matrix = [[1, 3, 5, 7], [10, 11, 16, 20], [23, 30, 34, 60]], target = 13
Output: false
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- -10^4 <= matrix[i][j], target <= 10^4
Explanation
Brute force approach
A naive approach is to traverse the matrix and search the target one by one. Run nested for loops and check every element with the target. If we find the target element, we return true or false.
The C++ snippet of this approach is as follows:
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if(matrix[i][j] == target) {
return true;
}
}
}
return false;
The time-complexity of the above approach is O(N^2).
Binary search
As per the problem statement, the matrix elements in each row are sorted from left to right. Which makes it easy to use binary search in a row.
But how do we find which row we need to search the element? Another property the matrix carries is that every first integer of each row is greater than the last element of the previous row. Which means the column is also sorted from top to bottom. We apply binary search on the first column.
Let's check the algorithm first.
// searchMatrix function
- set l = 0, m = matrix.size, n = matrix[0].size
r = m - 1
int mid
- loop while l <= r
- set mid = l + (r - l) / 2
// if the element is present in the middle row of the matrix
// we execute a binary search in the middle row
- if target >= matrix[mid][0] && matrix[mid][n - 1]
- return binarySearch(matrix[mid], n, target)
- if target < matrix[mid][0]
- set r = mid - 1
- else
- set l = mid + 1
- while loop end
- return false
// binarySearch function
- set l = 0, r = n - 1
int mid
- loop while l <= r
- set mid = l + (r - l) / 2
- if row[mid] == target
- return true
- if target < row[mid]
- set r = mid - 1
- else
- set l = mid + 1
- while loop end
- return false
The time-complexity of this function is O(log(n) + log(m)), and the space complexity is O(1). n is the number of columns and m is the number of rows in a matrix.
Let's check our solutions in C++, Golang, and Javascript.
C++ solution
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int l = 0, m = matrix.size(), n = matrix[0].size();
int r = m - 1;
int mid;
while(l <= r) {
mid = l + (r - l) / 2;
if(target >= matrix[mid][0] && target <= matrix[mid][n - 1]) {
return binarySearch(matrix[mid], n, target);
}
if(target < matrix[mid][0]) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return false;
}
bool binarySearch(vector<int>& row, int n, int target) {
int l = 0, r = n - 1;
int mid;
while(l <= r) {
mid = l + (r - l) / 2;
if(row[mid] == target) {
return true;
}
if(target < row[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return false;
}
};
Golang solution
func searchMatrix(matrix [][]int, target int) bool {
l, m, n := 0, len(matrix), len(matrix[0])
r := m - 1
var mid int
for l <= r {
mid = l + (r - l) / 2
if target >= matrix[mid][0] && target <= matrix[mid][n - 1] {
return binarySearch(matrix[mid], n, target)
}
if target < matrix[mid][0] {
r = mid - 1
} else {
l = mid + 1
}
}
return false
}
func binarySearch(row []int, n, target int) bool {
l, r := 0, n - 1
var mid int
for l <= r {
mid = l + (r - l) / 2
if target == row[mid] {
return true
}
if target < row[mid] {
r = mid - 1
} else {
l = mid + 1
}
}
return false
}
Javascript solution
var searchMatrix = function(matrix, target) {
let l = 0, m = matrix.length, n = matrix[0].length;
let r = m - 1;
let mid;
while(l <= r) {
mid = Math.floor(l + (r - l) / 2);
if(target >= matrix[mid][0] && target <= matrix[mid][n - 1]) {
return binarySearch(matrix[mid], n, target);
}
if(target < matrix[mid][0]) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return false;
};
var binarySearch = function(row, n, target) {
let l = 0, r = n - 1;
let mid;
while(l <= r) {
mid = Math.floor(l + (r - l) / 2);
if(target == row[mid]) {
return true;
}
if(target < row[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return false;
};
Let's dry-run our algorithm to see how the solution works.
Input: matrix = [[1, 3, 5, 7], [10, 11, 16, 20], [23, 30, 34, 60]]
target = 3
// searchMatrix function
Step 1: l = 0
m = matrix.size()
= 3
n = matrix[0].size()
= 4
r = m - 1
= 2
Step 2: loop while l <= r
0 <= 2
true
mid = l + (r - l) / 2
= 0 + (2 - 0) / 2
= 1
if target >= matrix[mid][0] && target <= matrix[mid][n - 1]
3 >= matrix[1][0] && 3 <= matrix[1][3]
3 >= 10 && 3 <= 20
false
if target < matrix[mid][0]
3 < matrix[1][0]
3 < 10
true
r = mid - 1
= 1 - 1
= 0
Step 3: loop while l <= r
0 <= 0
true
mid = l + (r - l) / 2
= 0 + (0 - 0) / 2
= 0
if target >= matrix[mid][0] && target <= matrix[mid][n - 1]
3 >= matrix[0][0] && 3 <= matrix[0][3]
3 >= 1 && 3 <= 7
true
return binarySearch(matrix[mid], n, target)
binarySearch(matrix[0], 4, 3)
// binarySearch function
Step 4: l = 0
r = n - 1
= 3
Step 5: loop while l < r
0 <= 3
mid = l + (r - l) / 2
= 0 + (3 - 1) / 2
= 1
if row[mid] == target
row[1] == 3
3 == 3
true
We return to step 3
Step 6: return binarySearch(matrix[mid], n, target)
We return the answer as true.



Top comments (0)