Problem statement
Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the definition of LCA on Wikipedia: The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).
Problem statement taken from: https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/
Example 1:
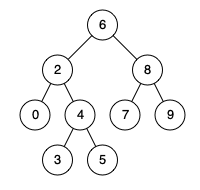
Input: root = [6, 2, 8, 0, 4, 7, 9, null, null, 3, 5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:
Input: root = [6, 2, 8, 0, 4, 7, 9, null, null, 3, 5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [2, 1], p = 2, q = 1
Output: 2
Constraints:
- The number of nodes in the tree is in the range [2, 10^5]
- -10^9 <= Node.val <= 10^9
- All Node.val are unique
- p != q
- p and q will exist in the BST
Explanation
Storing paths
The solution in this approach is to store the path from the root to p and root to q in two separate arrays. We then find the first element in the arrays that are mismatched.
For Example 2:
The path from the root to 2: [6, 2]
The path from the root to 4: [6, 2, 4]
We find the first element: 6 matches. We check the next element, which is 2, and it matches. The array for path root to 2 is done, and the array for path root to 4 has an element at the 2nd index; we consider it a mismatch.
We return the last element in both the arrays that match, which is 2.
A C++ snippet of the above approach is as follows:
bool findPath(Node* root, vector<int>& path, int k) {
if (root == NULL) {
return false;
}
path.push_back(root->val);
if (root->val == k) {
return true;
}
if ((root->left && findPath(root->left, path, k))
|| (root->right && findPath(root->right, path, k))) {
return true;
}
path.pop_back();
return false;
}
int findLCA(Node* root, int p, int q) {
vector<int> path1, path2;
int i;
if (!findPath(root, path1, p)
|| !findPath(root, path2, q)) {
return -1;
}
for (i = 0; i < path1.size() && i < path2.size(); i++)
if (path1[i] != path2[i])
break;
return path1[i - 1];
}
The time complexity and the space complexity of the above approach is O(n).
Single Traversal
We use preorder traversal and solve the problem using below steps:
- We check if the value of the root matches p and q
- If yes, we return the root
- else we recursively call the left and right subtree
- If there is any root that returns one NULL and one NON-NULL value, we return the corresponding NON-NULL value for that node.
- The root that returns both NON-NULL values for both the left and right subtree, is our LCA.
A C++ snippet of the above approach is as follows:
struct Node* findLCA(struct Node* root, int p, int q) {
if (root == NULL)
return NULL;
if (root->key == p || root->key == q)
return root;
Node* leftLCA = findLCA(root->left, p, q);
Node* rightLCA = findLCA(root->right, p, q);
if (leftLCA && rightLCA) {
return root;
}
return (leftLCA != NULL) ? leftLCA : rightLCA;
}
The time complexity of the above approach is O(n), and the space complexity is O(h), where h is the tree's height.
Recursion
The problem statement states that the tree is a Binary Search Tree (BST). We can modify the above recursive approach to avoid unnecessary calls to the left and right subtree.
Let's check the algorithm first.
- if root == null
- return null
- if root->val > p->val && root->val > q->val
- return lca(root->left, p, q)
- if root->val < p->val && root->val < q->val
- return lca(root->right, p, q)
- return root
This approach's time and space complexity are O(h), where h is the tree's height.
Let's check our algorithm in C++, Golang, and JavaScript.
C++ solution
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == NULL) {
return NULL;
}
if(root->val > p->val && root->val > q->val) {
return lowestCommonAncestor(root->left, p, q);
}
if(root->val < p->val && root->val < q->val) {
return lowestCommonAncestor(root->right, p, q);
}
return root;
}
};
Golang solution
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if root == nil {
return nil
}
if root.Val > p.Val && root.Val > q.Val {
return lowestCommonAncestor(root.Left, p, q)
}
if root.Val < p.Val && root.Val < q.Val {
return lowestCommonAncestor(root.Right, p, q)
}
return root
}
JavaScript solution
var lowestCommonAncestor = function(root, p, q) {
if(root === null) {
return null;
}
if(root.val > p.val && root.val > q.val) {
return lowestCommonAncestor(root.left, p, q);
}
if(root.val < p.val && root.val < q.val) {
return lowestCommonAncestor(root.right, p, q);
}
return root;
};
Let's dry-run our algorithm to see how the solution works.
Input: root = [6, 2, 8, 0, 4, 7, 9, null, null, 3, 5]
p = 2
q = 4
Step 1: if root == NULL
root -> 6
false
if root->val > p->val && root->val > q->val
6 > 2 && 6 > 4
true
return lowestCommonAncestor(root->left, p, q)
lowestCommonAncestor(->2, ->2, ->4)
// lowestCommonAncestor(->2, ->2, ->4)
Step 2: if root == NULL
root -> 2
false
if root->val > p->val && root->val > q->val
2 > 2 && 2 > 4
false
if root->val < p->val && root->val < q->val
2 < 2 && 2 < 4
false
return root
We backtrack to Step 1
Step 3: return lowestCommonAncestor(root->left, p, q)
lowestCommonAncestor(->2, ->2, ->4)
2
We return the answer as 2.


Top comments (0)