In this blog post, I go through the backpropagation algorithm, which sought to greatly simplify the training of neural networks. No single source could be solely accredited with its formulation, so I'd drop suitable links throughout this post pointing to the various sources from which this information was sourced
Unlike perceptron learning and thee Widro-Hoff learning rule, back-propogation can train non-linear networks of arbitrary connectivity. Back-propagation was developed with the aim of achieving a self-organizing neural network, where the general method behind how the network is trained did not rely upon specific network architectures (hence arbitrary connectivity)
Background Theory
a.k.a. crash-course on neural networks
A neural network is simply a collection of neurons, linked in some (usually pre-defined) manner, which is tasked with some sort of problem. Usually, we wish for our neural network to to e.g. predict whether an image is a cat or a dog (a classification task, with our classes being cat or dog* or predicting the likelihood of an airline passenger being satisfied, given quality of food, length of flight, etc (this is known as a regression task, where we are trying to predict some continuous variable).
Training a Neural Net
In order for our neural network to learn this input-output mapping, its internal weights must be set using existing data. We are essentially trying to fit
where represents our entire neural network, and is our labelled data. This is done by by maximizing log of above (i.e. ).
Since our data does not depend on the network,it is sufficient to maximize alone (which means that we can safely ignore attempting to calculate the marginal term in the denominator, which can get pretty ugly real fast)
Forward Propagation
The input is presented to network, and this input signal is propagated up the network, being multiplied by the weights of each layer, summed, passed through an activation function, and then passed to the layer above. In other words, the input to a given layer is a function of the outputs of the previous layer, parametrized by the layer's weights (this is the forward-pass).
Mathematically, inputs to layer are a sum of the inputs from layer multiplied by the weights
Outputs usually have some activation function such as:
The above function is not strictly necessary, since any input-output function with a bounded derivative will suffice (however using a linear function greatly simplifies network training)
Our network aims to learn the relationship between and if and are ordered pairs of data and outcomes.
Error Function
In order to adjust our layer weights (i.e. train our network), we need to quantify the difference between the network output and actual, ground-truth . To do this, we use an error function. Shown below is one of the more common error functions, however this changes depending on the task at hand, problem domain, etc.
The "Back" Part
If the error between network output and expected output is
we minimize by the method known as gradient descent. This involves taking the partial derivative of the error function for each input-output tuple.
This is where the 'back' part of the backpropagation arises. This error value is used to simultaneously update the values (layer weights) of the neural network. As a motivating example, let's say we're attempting to minimize the following convex function.

Gradient descent would take the value of the gradient of our current position and use the direction (sign) of this gradient to 'nudge' our network towards the minimum (in the direction of the arrow).
The magnitude of our gradient would determine how much 'nudging' our network receives. In other terms, the steeper the gradient, the faster our algorithm will attempt to converge (higher adjustment to weights) and vice versa.
Notice that if we were on the other side of the minimum, the direction for descent would be reversed, however gradient descent would use the sign once again to push the network in the direction of the minimum.
For the purposes of our neural network, the backward pass computes the partial derivative of each of its outputs' error functions. This error is then used to update the weights and is propagated to the higher layers in the network.
In other words, a layer just before the output would take into account the error seen by the output layer and adjust its weights according to the difference between its output and what the output layer was actually expecting. This process repeats all the way to the top of the network.
Tangent: Compared to a polynomial regression, a neural network may be able to adequately describe input-output relationships with only a subset of these polynomial features not known beforehand. In other terms, the neural network learns which features are important and boosts the weights responsible for these features
Finding Partial Derivatives
To find these partial derivatives, the chain rule is used. If our loss function at the (output) layer is , the partial differential with respect to the layer weights can be found using the chain rule.
Essentially, the differential of the output of a given layer with respect to layer weights can be gotten from the partial differential of the output with respect to its inputs multiplied by the partial differential of the layer inputs with respect to the layer parameters. Mathematically:
The above says that we can take a series of nested differentials starting from the output layer ending with the input layer. The error term is propagated down the layers in order to tune the hidden parameters throughout the network.
It turns out that back-propagation falls under a general set of techniques called automatic differentiation. This describes a set of elementary arithmetic (addition, multiplication, , , etc. The chain rule as described above can be used to find the gradient of complicated functions which differentiates the entire neural network, one layer at a time, as a function of the preceding layer. Let's break that down:
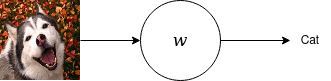
In the image above, let's say we're trying to predict whether an image is a dog or a cat, and we have a single-neuron single-layer network. On the forward pass, we show this network an image of a dog, it takes this input, multiplies it by its weights and produces the prediction. From the picture, it's clear that that image is not what the network predicted!

We then use the magnitude and direction of the difference in the output, to influence by how much the weights of the neural network should change to start predicting the correct output.
Now let's extend this to a multi-layer example. Same as above, our multi-layer network attempts to predict what the picture we show to it is, and again our network has not been trained as yet, and hence produces the wrong label (again, it's not a cat!)
In this case, the error at the output is used to change the weights at this last, top layer. But now, this change in the last layer directly influences how much the weights in the layer preceding layer changes. This is the back part of backpropagation, where the difference in what the last layer expects and what is shown to it by the middle layer is used to update the weights of that given middle layer .
This process continues all the way down the network until this error experienced in the output is used to indirectly correct the weights in .
Restating everything above, the differential of the loss function at each layer (starting from the topmost) with respect to the layer weights, tells us by how much and in what direction the layer weights should be updated.
Issues with Backpropagation
Vanishing gradients
As shown in the diagram above showing back-propagation and gradient direction, the closer the algorithm reaches to a near-zero error, the smaller our gradient becomes. As the algorithm progresses to the lower (input) layers, the weights for these layers can be left virtually unchanged, meaning our network is left untrained.
Exploding Gradients
The opposite to the above may occur if, for-example, instead of moving towards the bottom of our error function, our algorithm jumps completely to the other side of our error function. This results in the network having undefined parameters, which essentially means that all parameters in our network overflow on both sides of the number line.
These problems still face neural networks if left unchecked, and illustrate the tendency of neural networks to be trained in an unstable manner, where each layer learns at widely different speeds
Tangent: a 2010 paper found the combination of the logistic sigmoid activation function and the weight initialization technique popular at the time (a standard-normal distribution) caused the variance of the outputs of each layer to be orders of magnitude higher than the layers' inputs. This variance increases going up the network, eventually saturating the activation functions leading to the aforementioned problems. As an aside, the hyperbolic tangent function was found to behave more stably
Overfitting
The ultimate measure of success is not how closely we approximate the training data, but how well we account for as yet unseen cases of input. If a neural network is too large in comparison to the size of its input (in number of individual input matrices/tensors), it is possible for a sufficiently large network to merely "memorize" the training data. We say that the network has truly "learned" the function when it performs well on unseen cases.








Top comments (1)
You start with Baye's theorem and you reshape it to multiplication instead of division with P(D)???