In my previous post, I went through the basics of what anomaly detection is, why it is important and current challenges in the field. To give a TLDR
An outlier is generally considered a data point which is significantly different from other data points or which does not conform to the expected normal pattern of the phenomenon it represents
Distance-Based Approaches
A distance-based approach to anomaly detection is one which relies on some measure of distance, or distance-derived metric between points and sets of points. This results in multiple concepts of distance-based anomaly detection:
Less Than p Samples
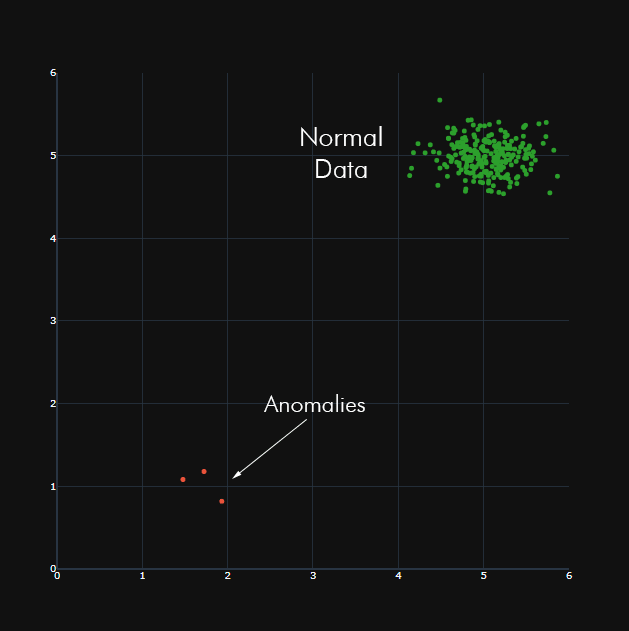
In this approach, points with less than p neighbouring points are classified as anomalous or outliers. For example, in the image below, the test point at the bottom left may be classified as anomalous based on the neighbour distance (represented as the dashed circle) and the number p, which is chosen depending on how sensitive the algorithm must be to anomalies. For example, very high levels of p will result in high numbers of anomalies, since few points may have the necessary numbers of neighbours within its radius of consideration.
kNN Methods
Distance to All Points
This the simplest possible method, where an algorithm evaluates a single point against every other point. The sum of the distances may be used as the metric. However, computing the scores of all the data points is generally computationally expensive intensive since all pairs of distances between points need be calculated. This is in all cases very expensive when the number of data points is large.
Distance to Nearest Neighbour
This is simple but can be misleading at times. A new point is considered anomalous if the distance to its nearest point is greater than some threshold.
Average Distance to kNN
In an unsupervised approach to anomaly detection, it is impossible to know the correct value for k for any particular algorithm, as this is highly dataset-dependent. A range of values of k may be tested. The average to a test point's k nearest-neighbours is less sensitive to different choices for K, since it effectively averages the exact k-nearest-neighbour scores over a range of values.
In the image below, depending on whether the distance-to-furthest OR average distance-to-furthest is used, the encircled point may or may not be considered as an anomaly.
Median Distance to kNN
This is very simple to interpret in low dimensions. It is additionally useful for building models that involve non-standard data-types, such as text. However, unlike the above, there is no standard way to choose k (except through cross-validation, etc), is computationally expensive and requires large storage requirements.
Pruning Methods
This can be thought of an extension to the aforementioned, with the main goal being a reduction in computational complexity. Pruning methods first partition the input space into discrete regions, with summary statistics such as the minimum-bounding rectangle, number of points, etc. During the nearest-neighbour search, a test example is compared to the bounding rectangle within which it lies, to determine first if it is possible at all for a nearby region to contain neighbours. If not, the region nearby is eliminated. This reduces the search complexity of actually finding nearby points to run distance calculations.
Metrics
There are multiple methods to determine the "distance" in distance-based methods, following are a few of the most common
Euclidean
This is possibly the most common, and is the easiest to work with. The Euclidean distance works well for well-clustered data, but is very sensitive to outliers. It may seem counter-intuitive to consider a metric's sensitivity to outliers when the entire point of anomaly detection is in detecting outliers, however an overly-sensitive metric may result in an unbearable false positive rate.
In all equations, assume that p and q are two points with i dimensions
Weighted Euclidean
If the relative importance of a dimension (which represents a feature in a dataset), then weighted Euclidean distance can be used. For example, if attempting to determine whether readings from a car's engine are anomalous, the oil-temperature may be far more important than the noise its engine makes. In other terms, more weight must be placed on the oil-temperature, since less variability is to be tolerated, whilst the sound in decibels can be down-weighted since it may have a wider operating range.
Minkowski
This is a generalization of the Euclidean distance, and similarly performs well for isolated, well-clustered data. However, large-scale attributes will dominate smaller-scale attributes (owing to the index term), hence caution is advised in terms of feature-scaling.
Manhattan
This is incredibly sensitive to outliers. The Manhattan distance results in a radius surrounding points which are hyper-rectangular (rectangular in high-dimensions). The caveat in using the Manhattan distance is that anomalies may be a function of both orientation and distance, which is not typically desired
Mahalanobis
This is most applicable when the dimensions in each axis are wildly non-comparable. This was originally derived to define regions that were hyper-ellipsoidal, and can alleviate distortion caused by linear correlation amongst features (this is known as a whitening transformation). However, this is incredibly computationally expensive, and should be used only when absolutely
necessary.
Advantages of Distance-Based Methods
- These methods scale well for large datasets with medium-to-high dimensionality
- These are also more computationally efficient than corresponding density-based statistical techniques
Disadvantages of Distance-Based Methods
- Extremely high dimensionality drastically reduces performance due to elevated computational complexity
- The search algorithms for nearest-neighbour methods can be inefficient unless a specialised indexing structure is used (such as a k-D Tree), at the cost of increased storage.
- Distance based methods cannot usually deal with data streams ad may not detect local outliers (such as between clusters of data points), since only global data is present








Top comments (0)