How to solve Graph Coloring problem using Backtracking

What is Backtracking ?

Backtracking is nothing but its a technique based on algorithms. It uses recursion to find the solution step by step increasing values with time and also it removes the solutions which don’t rise the solution based on constraints given in problem.

This backtracking is used in depth first search,graph coloring, Hamiltonian cycle.

What is graph coloring?

In graph coloring problem we color the vertices of graph in such a way that no two adjacent vertices or neighboring vertices share the same color. Same vertices can be colored in different ways so there are more one solutions possible here we want all possible solution what are the ways that can be colored so its like a permutations or trying out all possibilities and then picking up the one which are satisfying the condition, so the condition is neighboring vertices should not have same color so this type of problem can be solved using Backtracking then if you want multiple solutions and there is a different possible solution go for backtracking.

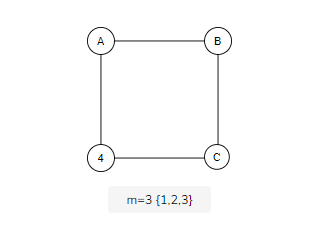
In this problem we have given a chromatic number m which is the least number of colors needed to color a graph.

EXAMPLE:

Now we take a simple graph and show you how this can be solved by using backtracking

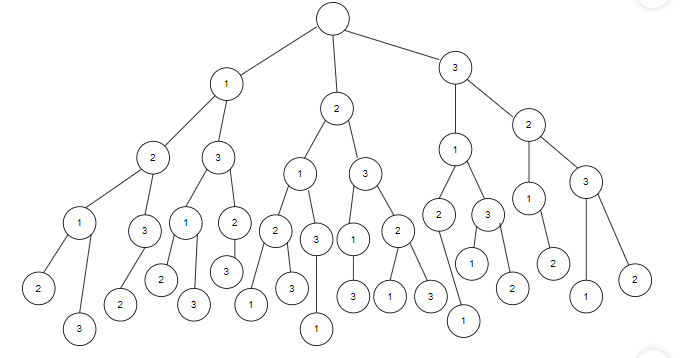
STATE SPACE TREE:

EXPLANATION:

1. State space is tree is mainly used to find out all possible solutions of the graph which satisfies constraints.
2. Initially A has the possible cases 1,2 and 3 if A takes the color 1 then B has two cases, and adjacent is 1 remaining two colors are 2 and 3 .Similarly this procedure is followed for vertices 2 and 3.
3. Suppose B is colored with 2 then C has two cases either 1 and 3
4. Now for D, A is 1 and C is 1 so possible combinations are 2 and 3.
5. For example in the above tree C is 3 ,A is 1, B is 2 so the adjacent are 1 and 3 only possible case is 2.
6. In the 3rd level A is 1 ,B is 3 and only adjacent is B,B is called 3 so the only possibility are 1 and 2. SO, C color is 1 and A color is 1 so two cases are 2 and 3. And A color is 1, B color is 3 and C color is 2 so, A and c are adjacent vertices, A color is 1, C color is 2 so remaining color is 3.
7. Second level represents all the possible colors which can be placed in vertex A.
8. Third level represents all the possible colors which can be placed in vertex B.
9. Fourth level represents all the possible colors which can be placed in vertex C.
10. Fifth level represents all the possible colors which can be placed in vertex D.

The chromatic number of the graph is 3(the minimum number of colors required to satisfy this problem).