In my last post I went over how to do a breadth-first search. In this lesson we're going to be looking at how to traverse a tree structure using a depth- first search(DFS).
As the name implies, this method of traversal focuses on navigating the tree data structure vertically. We start from the top and work our way down in columns. In general, you want to use DFS when finding an answer that has only one solution. An example of this is a chess AI finding the best possible move.
Unlike BFS, DFS has three different variations, pre-order, post-order, and in-order. Let's code out how to do each method, starting with pre-order traversal. For pre-order, we will first visit the parent, then the left and right children.
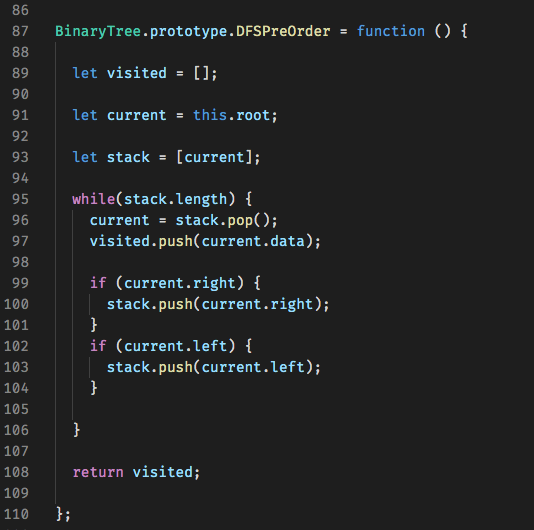
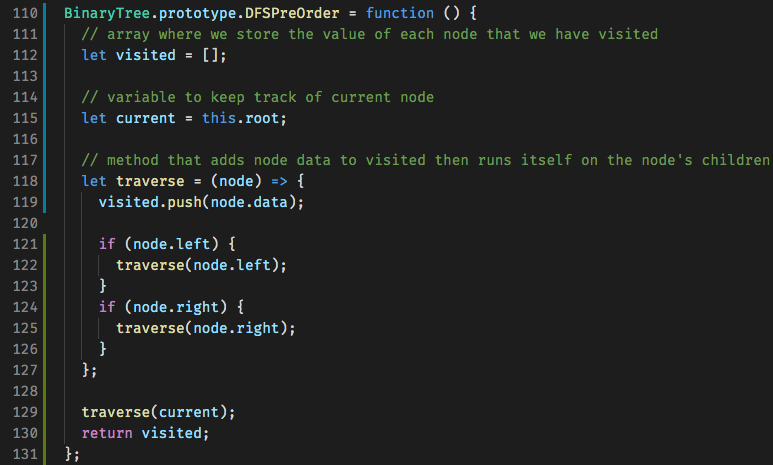
There are actually two different ways to go about implementing these methods. You can choose between using iteration and a stack or using recursion. I'll give an example of both for pre-order but will only use recursion for post-order and in-order because that's my preferred method.
For the iterative solution, we start by extracting the last node from the stack and adding its data to our visited array. We then add any of the node's children to the stack and repeat the process until we've worked our way through.
Notice that we first add the right node to the stack. This is because a stack uses the First In Last Out principle. Since we want to traverse all the way down the left side of the tree before making our way to the right we want the left node to be added to the stack last.
As for the recursive solution, we create a helper method named traverse that adds the node's data to our visited array and then runs itself on the node's left child, then the node's right child.
Post-order is the opposite of pre-order. We start at the bottom and work our way up to the top. To change our implementation we just push our node's data after traversing it's children.
In-order also works its way from the bottom up, but instead visits the parents before the children. This can easily be done by pushing our node's data after the left traversal but before the right traversal.
If you want to see the code from any of my tree posts you can view it here.









Top comments (0)