Hi Devs,
In the previous article we have discussed the Selection Sort algorithm and in this one, we will learn & understand the Bubble Sort algorithm.
Bubble Sort
Bubble Sort is the simplest sorting algorithm from the others because its working procedure is very easy to understand.
In this algorithm, we do two things.
compare two adjacent elements.
Arr[i] > Arr[i+1]for ascending order
Arr[i] < Arr[i+1]for descending orderand swap them if they are incorrect order (ascending or descending).
in each iteration, each element of the array moves to the end of the array.
let's visually understand this algorithm.

now, we are going to sort this array in ascending order using the above two steps or bubble sort algorithms.
compare two adjacent elements. and swap them if Arr[i] > Arr[i+1]

5 is less than 9, it does not satisfy the swapping condition just move forward.
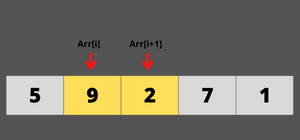
9 is greater than 2,it satisfy the swapping condition then swap them.
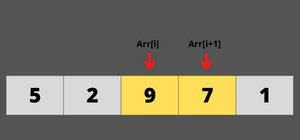
9 is greater than 7,it satisfy the swapping condition then swap them.

9 is greater than 1,it satisfy the swapping condition then swap them.

In the first iteration, we placed one element of the array in its correct position.
The same process will be follow until the last iteration.
after the last iteration,Array looks like this.
See the java Solution.
Java
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int[] arr = new int[]{5,9,2,7,1};
System.out.println("unsorted Array : "+Arrays.toString(arr));
bubbleSort(arr);
System.out.println("sorted Array in ascending order : "+Arrays.toString(arr));
}
private static void bubbleSort(int[] arr){
for(int i=0; i<arr.length;i++){
for(int j =0;j<arr.length-i-1;j++){
if(arr[j] > arr[j+1]){
swap(arr,j,j+1);
}
}
}
}
private static void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
Pros & Cons
good for the smallest data sets.
its easy to implement.
it will take more than n swaps.
not require any extra memory.
required more time to sort.
Time Complexity
In the worst case, the Time complexity of this algorithm
will be O(n^2).
bcoz it required two nested loops for comparing & swapping the two
adjacent elements.
Space Complexity
Bubble sort does not require any extra memory for sorting.
then, Space Complexity will be O(1)
Thank you for reading this article. share this article with your dev friends and save it for the future.








Top comments (0)