8 dont's and do's when writing a chatbot

Everybody loves chatbots. Here and there, online magazines proclaim the year 2019 as the year of the chatbots - exactly as they did for the years 2018 and 2017. In blogs, at the conferences, in the success stories, we hear about the unbelievably intelligent chatbots, incredibly successful startups, and unimaginable scientific advances. Big Tech keeps up the pace: Microsoft released their chatbot framework and natural language processing tools, Amazon did the same, and Google seems to make an even bigger step with Duplex, which calls the doctors or restaurants on your behalf to book you a table or an appointment.

Hearing and reading all this, you suddenly decide that maybe you should have your own chatbot. Perhaps, you’re not thinking of something too trivial, like Slack chatbot to initiate deployment. But, on the other side, you probably don’t feel like starting a whole new business around your idea. It’s something in the middle - the chatbot for your travel agency, or insurance company, or retail or restaurant, that allows booking tables or canceling journeys or other stereotyped actions without putting the pressure to your contact center. That would also entertain your customers and show your investors that you are on the right track of digitalization, artificial intelligence, and other High-tech stuff.

And it doesn’t even look so complicated, especially after hearing about all these advancements these days. People often think that artificial intelligence is basically here, ready to be hired, and after a little onboarding it will work for you, it will be intelligent and funny and charming, so the customers will buy your stuff just out of the pleasure of speaking with it.

This picture is, of course, fundamentally wrong.

For the last year, I completed one chatbot project, was directly involved in 2 more, consulted on a few more, tested tens and read about even more. None of them is intelligent and many of them are just bad. And one of the biggest reasons for them being bad was a huge misunderstanding between the management and the developers, mainly around the very basics: what the chatbot is, and how and who should develop it.

I would like to share with you some lessons I have learned during this year, the lessons that would help to make your chatbots better, although, still not intelligent. So this is not an article of yet another scientific technique, but rather more down-to-earth advices. It would be useful for product managers who would like to extend their knowledge on this topic, and also for data scientists or developers to avoid the potential pitfalls.

Don’t get overexcited

Yes, this is the first advice, plain and simple. Don’t be overexcited. The stakes are, your chatbot is not going to be intelligent in any way.

The problem is, the AI is not really here for hire. First, artificial intelligence is far less advanced in the field of NLP than in most other fields.

When we look at the Duplex presentation or use Google Translate, we think the AI behind these services understands the text. How else would it translate it? Well, in a way these services understand the text: the transform it into a vector representation (seq2vec) that essentially captures “meaning”, and use this representation to generate an output. However, the representation is specific to the task, the “meaning” is not universal, so it cannot be directly used for your needs. You can still use this representation to extract your “meaning”, but it is a data science task itself, and as such, it requires data, preferably lots of it.

And in many setups, the solution of this task is time-consuming, demands a lot of other resources and does not provide a significant improvement in comparison with more traditional approaches, like logistic regression on features based on words or letter-grams. These approaches are quite unintelligent but cheap, fast and effective.

The same applies to dialog management: yes, you can spend lots of money and time to create a truly intelligent chatbot, but the less intelligent and more traditional approach is simply more effective. So in the current state of the field, the intelligence has large costs and often the simply won’t pay off.

The good news is, customers do not really need this intelligence. Sometimes when we are overexcited, we think customers will deviate much from the flow we designed. We think they will demand sushi in a pizzeria - and we expect the good chatbot tho persuade them to order pizza instead of saying “Sorry, it’s not in the menu”. We imagine the customers to order delivery but won’t provide the address - and the chatbot would delicately handle the situation, arranging the delivery to the bus stop. We fantasize about customers asking whether the chatbot is married and try to flirt with it - and for some reasons think that if the chatbot will play along, the customers buy more.

My experience is that it is simply not true. Sure, some people will try to expose the stupidity of the chatbot, but they are not real customers, they are just looking for fun, and it’s not so many of them. At least in Germany, where I work, people are generally ready to comply with the chat flow you provide, if the flow makes sense. Some fringe cases are possible, but they simply do not worth the effort.

The only stage of the conversation, where the deviations are possible and probable, is the very first step when the chatbot tries to understand what the customer wants. No matter how well you design the description of the chatbot capabilities, people won’t read it and will try to address all their grievances to the chatbot, some of them being truly unique and unpredictable. You can’t really do anything with it, except for the famous “Sorry, I don’t understand”. The best strategy here is to handle the conversation to the person behind the chatbot.

Also, no one in Germany is going to socialize with the chatbot. I suspect this depends on the culture, but in Germany, there is no need in “small talk”, the feature that is discussed among chatbot developers quite extensively. In one of the project, we have spent quite a time planning and implementing chatbot small talk, only to find out that there was not a single person in weeks trying to access it. So instead of the feature that engages customers, it turns out into an exotic Easter egg only a dedicated customer could find.

And the last point is, there is simply not so much intelligence required when booking a plane. The customer should answer some specific questions, then the API call should be made, and the ticket should be provided to the customer - and that’s it. Imagine it would be implemented as a form on your web site - who on Earth would call it intelligent? If no one, why should this form suddenly become intelligent simply because it’s now implemented as a chatbot? The intelligence is determined by the service and not by the format. Of course, you could think about the chatbot that would not only sell tickets but also helped to choose the best location for vacations, depending on customers preferences. This service would indeed require some “artificial intelligence”. But such service will not appear simply because of your booking service is now implemented as a chatbot. It would be a different project, that I could call a “power-chatbot”, so it would require other approach and way bigger budget - it would be better considered as a standalone startup rather than an auxiliary project.

Sometimes it is hard to draw a line between the power-chatbots and the common ones. The criterion could be this: are you trying to do something that no one did, or something that everyone does? So if it is the second kind of the project for you, it could help not to confuse it with the first kind, and not to use the means for the first kind. It can be really hard, because most of the papers and conferences talks are about power-chatbots, and that sometimes creates a pressure from the management: hey, why aren’t we just using the stuff everyone is talking about instead of all this?! The answer is, the projects are different and therefore solutions are, too.

But if these common chatbots are not so intelligent, and the customers do not need it anyway, what this all is about?

Instead of focusing on intelligence, try to perceive the chatbots as yet another channel to reach the customers. Some considerable time ago, every business created web-page to reach the customers on the internet. They, when mobile phones become available, we learned that people do not like so much to visit the websites via mobile internet so much, preferring application - so lately the businesses developed the mobile applications. Recently we discovered that customers are fed up with hundreds of applications on their phones, and are not going to install yet another one - so we try to reach the customers via the application they already have, the messenger. And that’s it. The chatbot is an interface that allows your business to deliver services over this media, not the customer’s soulmate.
The next “big thing” seems to be the voice assistants, and already today you can create the skill for this assistant. Natural language generation and sometimes even natural language understanding are often already implemented, so the dialog management is the only thing to develop. This is a reason why the chatbots are probably going to stay in focus for awhile - they are interfaces not only for messengers, but also for voice assistants.

Don’t do deep learning

Deep learning is the primary enabler of all the recent accomplishments in natural language processing, as well as behind the power-chatbots. So the overexcitement about the whole topic would certainly tip the scales for this particular technology, but I hope we already sort that out in the previous paragraph. The deep learning also has its own advantage: you might hear promises, that regardless of the chatbot complexity, deep learning would allow you to avoid programming in your project - the chatbot will magically, by itself, learn the conversation flow. Or, more accurately, the neural network will observe lots of existing conversations, and then understand their hidden structure and how to deliver them, including new cases that were not directly observed, but follow the same patterns.

That might indeed happen, but, as I have said, the artificial intelligence has costs and requirements. First, do you have enough data? Like, thousands of conversations? Are these conversations relevant - because we don’t message exactly in the way we speak over the phone? Do you have the customer’s consent to use these conversations for this purpose? If the conversations are audio files, they have to be converted into text - do you know the costs and do you have consent to transfer the data to the third party for processing?

And even if you do have the data, the next question is: don’t you know the conversational flow already? If you can just sit and draw the conversation, just do it. That’s perfectly fine!

Yes, for some problems, we can’t. Imagine the conversation with a medical doctor. Question after question, all of them related and dependent on the gigabytes of medical knowledge. This is indeed impossible to directly encode, thus the scientists are trying to find the means for this task. But if this is the conversation about ordering the pizza - mighty neural networks won’t come up with anything fantastic, simply because there is nothing fantastic to come up with! It would be cracking nuts with a sledgehammer - also with a very fragile and expensive one.

Don’t directly encode state machines

Once you gave up on deep learning, you will probably stay with a good old state machine approach. This is a perfect way to define the conversation, it is very easy to explain and to understand, allows a good graphical depiction, and also has a sound mathematical model behind. So there is a temptation to use this model as the software architecture for your chatbot as well.

This would be, however, a grave mistake. Very soon you will find yourself in a hell of “if’s”, “else’s” and global variables, a hell you will find quite hard to escape. So you can only do it if you develop a very small chatbot, with the understanding you’ll have to throw away all of this code once there is a need to expand.

If the chatbot has several skills, and the skills are non-linear, I would definitely suggest to invest some time into figuring out the best way to encode the state machine. That could be, for instance, UML diagrams that are executed by a library. Myself, I prefer more code-based approach, so I came out with something like this:

def TraceDelivery(context):
    trackId = None
    for i in range(3):
        yield Prompt(Vocabulary.EnterTrackId if i==0 else Vocabulary.ReenterTrackId)
        yield Listen()
        if is_valid_track_id(context.input):
            trackId = context.input
            break
    if trackId is None:
        yield Prompt(Vocabulary.UnrecoverableFailureAndHandover)
        yield HandOver()
    context.slots['trackId'] = trackId

The chat flow is a generator function. When your interpreter executes the flow, it creates the iterator and fetches commands from it until “Listen” command is found. At this point, it sends all the previous commands to the customer and waits for their reply. The reply is inserted into “context” variable, and the iterator resumes until the next “Listen”. Essentially, in this approach, the compiler will build the state machine itself.

This architecture has proven to be really extendable for more complicated use cases, for instance:

• If there is a need to break one scenario into the smaller part, you can return Subroutine command with the pointer to the next generator function. Once your interpreter obtains this command, it puts the current iterator into the stack, creates a new iterator from the scenario and executes it.
• Listen command can carry the information about what kind of input is good to continue with. If the interpreter receives the customer’s input that does not match, it drops or stashes the current iterator, and rolls back to some backup that processes the unknown inputs.
• If the external API calls are needed, the generator can produce the corresponding command and then receive its result as an input. That will separate API calls from the dialog management, simplifying logging and testing.

I thought about wrapping up this approach as a library but came to a conclusion it does not really worth it. The commands you use inside the scenario and the additional features are too dependent on the actual business case you work on.

Keep in mind this approach have several disadvantages:

• It can be implemented in many programming languages, but not in all of them. Generators feature is obviously crucial.
• In many languages, the generated iterator is not serializable, thus can only be stored in memory. It is not a big problem if the conversations do not last ages, and normally they don’t.

For the specific classes of the conversations there are GUI-based solutions you could find helpful, often along with natural language processing. For instance, there are multiple implementations for slot-filling dialogs, when the purpose is to fill some information about order: for instance, color, size, and neckline for T-shirt. Some of the information can be provided with the first utterance (“I want a red T-Shirt of size M”), some other retrieved with additional questions.

Don’t write unit tests

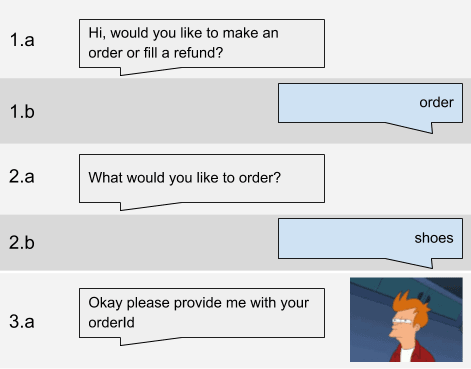
Unit tests are useful in many cases, but the dialog management is not one of those. Consider the following conversation:

Unit tests suppose to test atomic functionality, like the response of the chatbot to the specific input. We see, that the output at the 3.1 depends not only on 2.b, but also on 1.b. Hence, in order to reproduce the behavior in tests, the context information about 1.b should be injected into the test. That brings two problems:

• We can’t really inject the whole context, only the assumptions we have about it. We assume that stage 1 results, e.g., in the certain values in certain fields of the state. Are these assumptions controlled? If no, they will become invalid one day, bringing false-negative results, the worst thing imaginable in QA. But if yes, that means that after every test you need to check for both output and state changes thoroughly, which means the tests will become excessively time-consuming to write.
• When you express the assumptions in code, you lock the architecture: in order for tests to work, the chatbot must have the state, and this state must have certain fields with certain meaning. If you will want, at some point, refactor the state, you will have a problem: in order to refactor the code safely, you need to control its behavior, but the only means you have to control it prevents you from refactoring. This is a deadlock impossible to escape without writing a parallel set of architecture-agnostic tests.

So why not to start with such architecture-agnostic tests in the first place? It’s perfectly fine to opt sometimes for the testing means other than unit tests, especially if the reasons are good. So, integration tests are the perfect alternative for unit tests. Just construct the conversations your chatbot is supposed to handle, and check if it does handle them!

The total amount of all conversations is, of course, quite high, and this issue can be addressed as follows:

• If the chatbot has sane architecture, so different skills are independent and you are sure the composition operation works correctly, you can simply test skills and important parts of the skills.
• Alternatively, you can build a graph of all possible flows, generating linear scenarios by the depth-search in this graph. Such tests will take quite a time, but it’s a machine time anyway. The graphs also have its own value: they keep on track the design of the conversations, so you can relatively quickly remember how should it look like.

Integration tests also have two additional advantages:

• You can always show the management the list of conversations that certainly works
• You can do test-driven development: start with writing the conversation down as a test, and later find the implementation that passes the tests. In a good setup, product manager, or product owner, or whoever else responsible for the conversation design, might even write the tests for you!

Don’t forget about logging

It may sound bizarre, but yes, sometimes people don’t pay enough attention to the logging. This is especially bewildering for the voice assistants when we can’t even make a screenshot to reproduce an error. So I would definitely suggest not to repeat such errors and build a comprehensive logging procedure. Do not try to implement analytics and logs within the same module: log everything in the most primitive way, and then write scripts that parse and represent the logs, otherwise, you will never know if the error occurred in the dialog management or in the analytics module.

The good criterion of the quality of the logs is reproducibility: you have to be able to replay the log with the dialog management and obtain the same result. If you cannot figure out a way to do it, it is a good indication that either log does not contain some vital data, or the architecture of the chatbot is wrong.

A reproducible log is a valuable tool for QA engineers: instead of describing to you what they think happened, the can simply provide you with the timestamp of the error, so you can retrieve the problematic conversation, reproduce it, debug, and make sure that the error is really gone after you’ve finished.

Don’t underestimate Whatsapp

There are good, flexible messengers that are fun to work with, that provides API and tons of fascinating functions for the chatbot. And also there is Whatsapp. Gray API, terrible support, no functions. The immense misfortune is that it is the most popular messenger in Germany.

Whatsapp was recently bought by Facebook, so maybe, we will finally see some evolution, but right now you have to be conservative when estimating time for Whatsapp integration.

I cannot really provide you with any details about what exactly could go wrong, but both times I saw people doing something with Whatsapp, they were quite unhappy and went significantly beyond the planned deadline.

Don’t write your own annotation tool

Manual annotation of data is a task you can happily avoid for years, being nevertheless an awesome data scientist. For recommender systems, churn prediction or forecasting of business parameters, we simply have all the data in place. So it can be quite sudden to discover that for your chatbot you need:

• To indicate intent for a sentence, i.e. specify, that “I’m thinking about buying shoes” actually means “order”.
• To highlight the named entities, like “shoes” in the previous example.
• To evaluate the unsuccessful dialog that already has happen and to understand, why it failed.

So basically it looks quite simple: present the task to the annotators and collect answers. And at this point you probably think: what are we talking about, I would just sit and write a small tool, just a couple of hundreds lines of code, it’s simple!

Don’t.

Over my entire career, I’ve seen around ten of such homemade annotation tools. The vast majority of them took much more time to develop than planned, and nevertheless, they were ugly, dysfunctional, unmaintainable and discontinued at some point.

Fortunately, there is an alternative: Pybossa framework. It’s free in both senses, it’s self-hosted, so you don’t have to worry additionally about GDPR, it’s being actively developed and maintained. Creating a new decently-looking task within this framework will require around 1-2 days. A competent DevOps can deploy the system within a few hours, there are also dockerized versions available for development and testing.

Do not hire the team of data scientists for this job

Yes, you’ve read correctly, and I can also add: “maybe, even none of them”.
Most of the things we discussed aren’t data science - it’s pure software engineering. And since we are not talking about power-chatbot, there are a quite limited set of tasks data scientists could actually perform. It is the task of the intent recognition (to understand the text), named entity recognition (to extract the important information from user utterances), and, sometimes, ranking problem (to provide the best answer in response to customer question). The truth about these tasks is:

• It is really easy to get first acceptable results: the algorithms for that are well-known and well-implemented, there is nothing really “data-scientific” here, and a strong developer with a superficial interest to data science will manage.
• It is challenging to advance significantly beyond this first result. This advancement can take a lot of time without providing visible result in the end, because such improvements only affect the fringe cases. These cases are easier to avoid by other, non-coding means, such as writing helpful prompts that actually inform customer about what is happening.
• Google NLP and Microsoft LUIS provide ready algorithms for some of these tasks. I’d say the advancement in these areas will soon enough render any in-house development on the subject useless.
• For ranking problem and Question and Answer systems data scientists could still be valuable, but it only applies if you already have the data. If you don’t, hack together something minimally functional, run the system, collect the data and then hire the data scientist to improve the performance.

Hiring data scientists for such projects also have risks. From personal experience, they tend to undervalue issues of the software development side while paying too much attention to the complicated fringe cases and powerful algorithms to handle them, sometimes without assessing the business-value. Myself, I managed to avoid it, because I worked as a software developer for years before switching to data science. But not all data scientists come from this field. As a result, the direction in which the project progress will be skewed, sometimes catastrophically, and this is particularly a problem if the management do not really know what the data science is. So the best strategy for the management is to learn this, and another acceptable strategy to let the project to be driven by software engineers and not by data scientists. As in many other types of projects, data scientists should enhance a chatbot rather than build it from scratch.