Here we are again with another binary tree exploration! I hope you guys aren't bored with my focus on binary trees. They're so far one of the datatypes in my brief experience that I can understand due to their visual nature. I've always been a visual learner so it probably explains my affinity for them. But anyways, let's start tackling this problem!
Given the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node, down to the furthest leaf node.
I highlighted nodes in the prompt to avoid people getting as confused as I got when solving this problem. For this instance, when finding the maximum depth of a binary tree, we will be counting the nodes, NOT the edges.
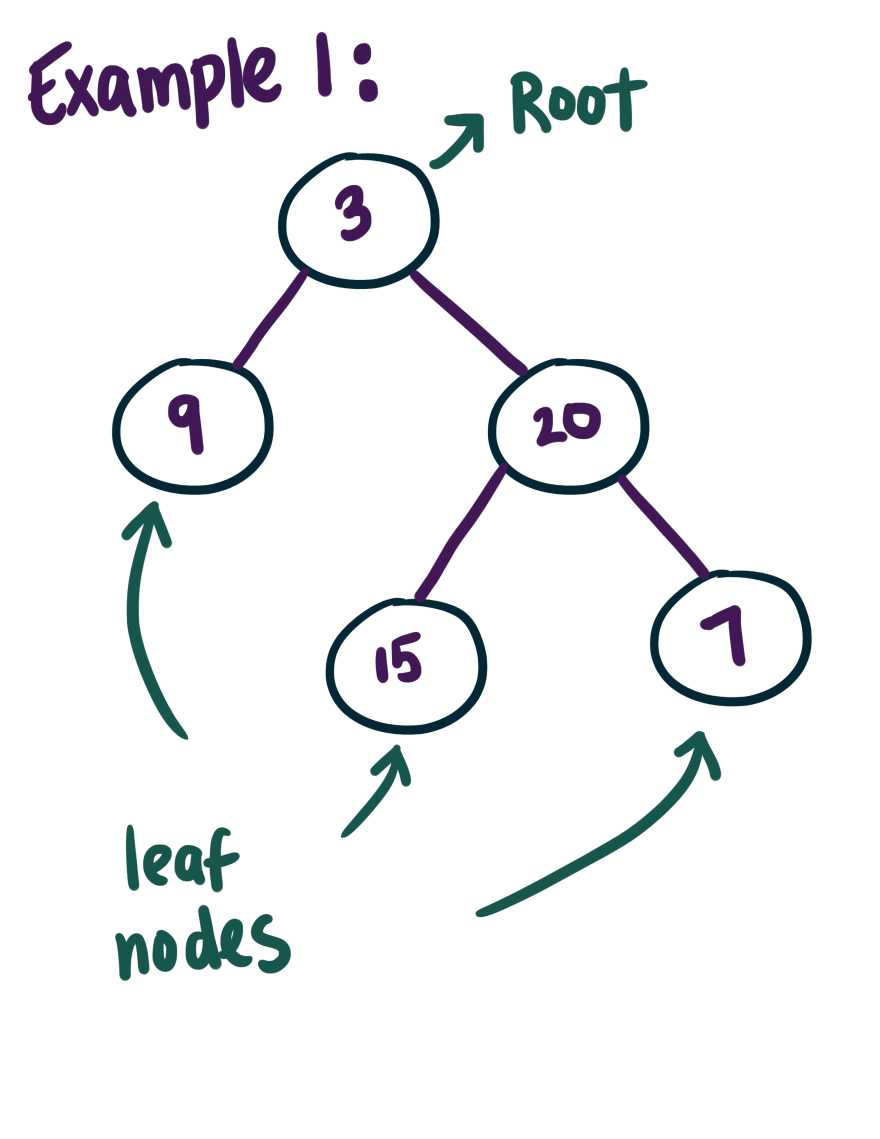
Let's look at the first given example to further understand what is being asked of us:
Leetcode wants us to start from the root node 3 and find the maximum depth. We have to traverse the binary tree from the root node, all the way to the leaf node that has the longest path. According to our example, our leaf nodes are 9, 15, and 7. From root 3 there are three paths: 3 -> 9, 3 -> 20 -> 15, and 3 -> 20 -> 7. If we count the nodes, paths 3 -> 20 -> 15, and 3 -> 20 -> 7 have the maximum depth of 3. Nodes 7 and 15 are the longest nodes with the same height. There are 3 nodes from the root to the farthest leaf node, hence the output will be 3.
We're going to solve this problem recursively using the Depth First Search, the same approach we used in my last post 100. Same Tree.
If we think about the base case, let's think about what would happen if we had an empty tree. If so, there would be no root node or leaf nodes to measure the depth, so the output would be 0.
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
What if we only had a root node and no children nodes? Then what? So we'd have a starting point to count from, so then we'd have to look at the maximum amount of the left subtree and right subtree. The maximum amount of both subtrees would be 0. The point of view from the root node will be 1 + (self.maxDepth(root.left), maxDepth(root.right)). By saying ' 1 + ' we're recording that if there is a root node, that it's been counted, so we can look past the root node to find the maximum path within the left or right subtrees.
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))
When we continue our search, we look to the left subtree which has a node of 9 with no children. This means the max depth of the left subtree is 1 so we add it the root node which has been counted already as 1. Adding them together gives the left subtree a maximum depth of 2.
If we look at the right subtree, we start the recursion over again. Node 20 will be the new starting point. Node 20 has a left subtree of 15 and right subtree of 7. Both 15 and 7 are going to each return 1. From the point of view of node 20, it will return 2 because of the return amount of its left and right subtrees (1 + 1). Finally we take the return maximum path value of the right subtree and add it with the root node 3 which has been counted as 1. Adding 2 (from the subtrees of node 20)+ 1 (the counted root) we receive the maximum depth of 3.
Since we are solving this recursively for the tree in its entirety, the time complexity of this problem will be O(n).
Conclusion:
I thought this problem was a great challenge for many reasons. It covers the concept of depth/height, allows us to review the process of recursion, and there are other many ambitious ways to solve this problem without recursion. For now, I'm happy with solving this problem with the Depth Search First recursion method because it makes the most sense to me as a novice algo solver. After dealing with binary trees for a few weeks, I'm starting to have a better insight as how to solve this specific datatype.
Resources:
https://www.educative.io/edpresso/finding-the-maximum-depth-of-a-binary-tree







Top comments (0)