There's a zillion blog posts attempting to explain Big O Notation, because we are all told that it's something we need to know for technical interviews and maybe--just maybe--we might even use it on the job at some point.
If there's so many blog posts about it, why have you written one?
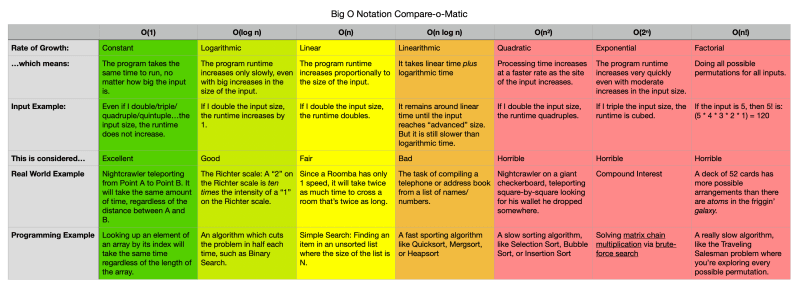
In my very long quest to understand Big O Notation, I've yet to come across a giant table comparing each classification starting with real-world examples and progressing to computer science examples. So I've tried to do that here.
Before we start, what's the deal with Big O?
Big O describes the efficiency of an algorithm, helping us answer the question: "Will this algorithm scale?".
So, how do you rate the efficiency of an algorithm?
By looking at worst-case scenarios. Algorithms are functions that accept inputs, right? The function never changes, but the input fed into that function could be tiny or gigantic or anywhere in between. So, looking at how long an algorithm takes to process a function (which will depend on the number of operations it takes to complete) in a worst-case scenario versus a best-case scenario is how we rate it's efficiency.
Ok, so, what are the different classifications?
I thought you'd never ask!
If you're adverse to downloading the .pdf above for some reason, what follows is a series of charts for each classification (because Dev.to has a viewport too narrow for my pretty chart)
| Classification | O(1) |
|---|---|
| Rate of growth | Constant |
| By which I mean | The program takes the same time to run no matter how big the input is. |
| For example | Even if I double/triple/quadruple/quintuple... the input size, the runtime does not increase |
| This is considered | Excellent |
| Real world example | Nightcrawler teleporting from point A to point B. It will take the same amount of time, regardless of the distance between A and B. |
| Programming example | Looking up an element of an array by it's index will take the same time regardless of the length of the array |
| Classification | O(log n) |
|---|---|
| Rate of growth | Logarithmic |
| By which I mean | The program run-time increases only slowly, even with big increases in the size of the input. |
| For example | If I double the input size, the runtime increases by 1 |
| This is considered | Good |
| Real world example | The Richter scale: a 2 on the Richter scale is ten times the intensity of a 1 on the Richter scale |
| Programming example | Any algorithm which cuts the problem in half each time, such as binary search. |
| Classification | O(n) |
|---|---|
| Rate of growth | Linear |
| By which I mean | The program run-time increases proportionally to the size of the input. |
| For example | If I double the input size, the runtime doubles |
| This is considered | Fair |
| Real world example | Since a Roomba has only 1 speed, it will take twice as much time to cross a room that's twice as long |
| Programming example | Simple Search: Finding an item in an unsorted list where the size of the list is N |
| Classification | O(n log n) |
|---|---|
| Rate of growth | Linearithmic |
| By which I mean |
|
| For example | It remains around linear time until input reached "advanced" size. But it is still slower than logarithmic time. |
| This is considered | Bad |
| Real world example | The task of compiling a telephone or address book from a list of names/numbers |
| Programming example | A fast sorting algorithm like Quicksort, Mergesort, or Heapsort1 |
| Classification | O(n2) |
|---|---|
| Rate of growth | Quadratic |
| By which I mean | Processing time grows faster and faster as the size of the input increases. |
| For example | If I double the input size, the runtime quadruples |
| This is considered | Horrible |
| Real world example | Nightcrawler on a giant checkerboard, teleporting square-by-square looking for his wallet he dropped somewhere |
| Programming example | A slow sorting algorithm, like Selection Sort, Bubble Sort, or Insertion Sort |
| Classification | O(2n) |
|---|---|
| Rate of growth | Exponential |
| By which I mean | The program run-time increases very quickly with even moderate increases in the size of the problem |
| For example | If I triple the input size, the runtime is cubed (like exponents, get it??) |
| This is considered | Horrible |
| Real world example | Compound Interest |
| Programming example | Solving matrix chain multiplication via brute-force search |
| Classification | O(n!) |
|---|---|
| Rate of growth | Factorial |
| By which I mean | Doing all possible permutations of the n elements |
| For example | If the input is 5, then 5! is 5 * 4 * 3 * 2 * 1 = 120 |
| This is considered | Horrible |
| Real world example | A deck of 52 cards has more possible arrangements than there are atoms in the friggin' galaxy |
| Programming example | A really slow algorithm, like the Traveling Salesman problem where you're exploring every possible permutation |
By the way, if you see any mistakes or have better/other examples/explanations, please share them in a comment!
-
As Erick Hagstrom explains in the comments below, "Heap sort...is O(n log n) because it works in essentially two phases. It first builds a heap in O(n), then adjusts that heap--sometimes referred to as sifting down--in O(log n). It takes linear time plus logarithmic time." Thanks for the clarification! ↩






Top comments (2)
Your explanation of "linearithmic" sounds as though it starts out linear, shifts to logarithmic at some point, but ends up worse than either. That is wrong. Heap sort, for example, is O(n log n) because it works in essentially two phases. It first builds a heap in O(n), then adjusts that heap--sometimes referred to as sifting down--in O(log n). It takes linear time plus logarithmic time.
Thanks for the clarification, Erick! I added a footnote with your explanation. Any other feedback?