Numpy is a powerful python package for three main reasons:
- python is slow and numpy is written mostly in C, one of the fastest languages ever created.
- Numpy is the backbone of other packages.
- It makes it easy to work with arrays and matrices.
The core of machine learning is to find patterns through a lot of numbers that's why numpy is essential.
Table of contents:
- Anatomy of a numpy array
- Creating arrays with numpy
- Useful functions and methods
- Randomness in programming
- Manipulating arrays
Anatomy of a numpy array
examples were taken by the machine learning course by mrdbourke
In machine learning our main focus will be on how the shape of our data will lines up with other data and outputs and numpy arrays, technically called ndarrays, or n-dimensional arrays, will be fundamentals.
Importing numpy
Wouldn't forget the most important thing, would you?
1 dimensional arrays
The first type of ndarray is the most simple: an array with just one dimension, usually called vectors:

Every array has a shape, that in this case is 1 and 3.
2 dimensional arrays
A 2-dimensional array is usually called a matrix, and is very similar to pandas dataframes:

Obviously, even the shape change.
3 dimensional arrays
The 3-dimensional array is when the concept of multi-dimensional array is really important. After this, an array is simply called an n-dimensional array:

Now the shape has even depth in it.

If you remember in the last post when I have mentioned the axis, this is where it gets important.
Creating arrays with numpy
We have seen the anatomy of an array in numpy, but, obviously, creating one always typing every value by ourselves would be inefficient and useless.
Example array
We can create a first example array with the function ones(), but if we use the shortcut shift + tab we can see what a function does without searching the documentation, that will instead appear under the function itself:

But that aren't enough informations. We can see more by clicking on the x to actually scroll all the document in the little window, or on the ^ to position the doc in the lower part of the screen:

And scrolling down, in this case, we can even see the examples of how to use the function:

Now we know what we can put into the function and what to expect:

We have defined the shape of the array and the output, corresponding to a table of two rows and four columns, or an array that contains two arrays, each one with four elements.
Why all ones?
Sometimes, before starting to work, we may want to be sure of the shape of our array, that's why we may want to create one filled with one or zeros - another numpy function - that create a simple array with an initial shape.
Useful functions and methods
In this section, we'll dive into the most useful functions and methods that numpy offers, for then to introduce the concept of random numbers.
Dtype
The dtype numpy method shows us the data type of the array.
Using the previous array:

Creating an array with a function, as in this case, the default type will be float64.
Type
The type function will simply show us what type of array we have, in numpy it will always result in a ndarray, as we have already stated:
Size
The size method will show us how many elements are in the array.
Shape
The shape function will show the shape of the array:
Ndim
The ndim method shows how many dimensions the array has:
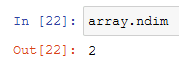
In this case, this array is a matrix, then 2 dimensions.
Arange
Arange lets us generate numbers within a range. Pressing shift + tab in the middle of the brackets we can read the doc to better understand what it does:
Docstring:
arange([start,] stop[, step,], dtype=None)
Return evenly spaced values within a given interval.
Values are generated within the half-open interval ``[start, stop)``
(in other words, the interval including `start` but excluding `stop`).
For integer arguments, the function is equivalent to the Python built-in
`range` function, but returns a ndarray rather than a list
But this, despite being very clear, it's too much wordy, if we see the examples
Examples
--------
>>> np.arange(3)
array([0, 1, 2])
>>> np.arange(3.0)
array([ 0., 1., 2.])
>>> np.arange(3,7)
array([3, 4, 5, 6])
>>> np.arange(3,7,2)
array([3, 5])
So the first argument is the beginning of the range, the second is the end and the third is the stepover, let's see it in practice:
Randint
We can create even random arrays in a range of numbers with the random.randint function.
Pressing the shift + tab we can read:
Docstring:
randint(low, high=None, size=None, dtype=int)
Return random integers from `low` (inclusive) to `high` (exclusive).
Return random integers from the "discrete uniform" distribution of
the specified dtype in the "half-open" interval [`low`, `high`). If
`high` is None (the default), then results are from [0, `low`).
But the best way is always to explore:

the first argument is by default 1, so if we just type a number and a shape into the function it will create values between 0 and the number that we put in it.
We have created an array with values that range between 4 and 9 and with a shape of 2 and 5.
Random
But if we want to just create a random array without a precise range, we can just use the random function. We have to enter just the shape:

random.random goes between 0.0 and 1.0.
Randomness in programming
A computer works only with binary values, 0 and 1, so how can a computer create random values?
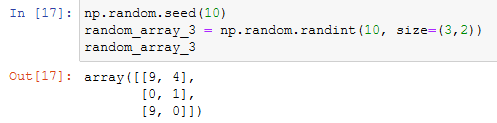
A computer creates pseudo-random values through a function called, by convention, seed. If we use always the same seed for random values, those values will always be the same, otherwise, numpy will always change the seed to create values that look random:

We can manually declare the seed so that even if the numbers are randoms when running the command they will always be the same because are based on the same seed:
Manipulating arrays
Numpy offers us a lot of ways to manipulate an array through a technique called broadcasting. Let's begin with creating new arrays that we can do our tests on:

With numpy, we can do basic arithmetic calculations, that we'll see now, and other things that we'll see in the second part:
Additions
We can perform calculus in arrays directly, using the operator, but, in some case, it may give a result that we don't want:
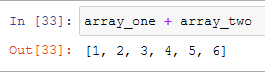
So it's better to use the dedicated functions that numpy offers:

And this is the result that we want, [1, 2, 3] + [4, 5, 6] gives us a third array with inside [5, 7, 9].
Subtraction
Without the function, we would have an error, but using it everything work as intended:

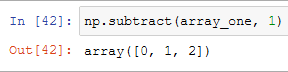
But when using a numpy function we don't have to just use arrays, we can even just lower all the elements of the array of one, or any number that we want:
division and multiplication
Using the dedicated numpy functions everything will work fine:
Floor division and power
If we don't want decimals when we divide our arrays we can use the floor division function that will return the array divided without decimals plus the type, that we don't want - we can fix it using the tolist function:

For the power of two arrays, it's the same thing:
Final thoughts
This was the first part on using numpy for machine learning, if you have any doubt feel free to leave a comment.




















Top comments (0)