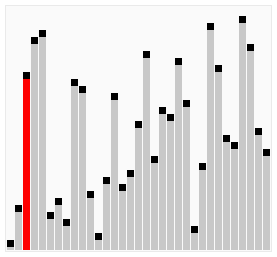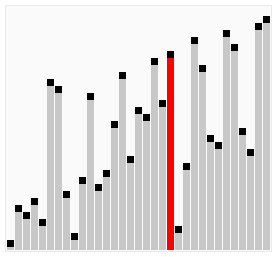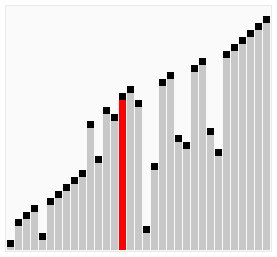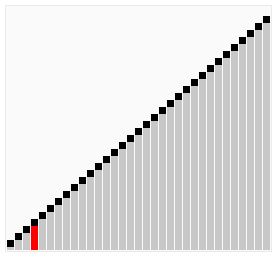
Today I want to talk about the first sort that I have learned, bubble sort. Approaches to sorting arrays are named in such a way that they illustrate what they are doing.
Bubble sort takes a look at the current value and the next value in the array as you iterate through it. If during your iteration you find that you have a current value greater than your next value you must swap those values.
Not swapping is not enough because we need to create something called a sentinel value. What a sentinel value does is it acts like a gate keeper. It controls the flow of your loop such that you need to continue looping while it is true or not true, depending on how you coded your sort.
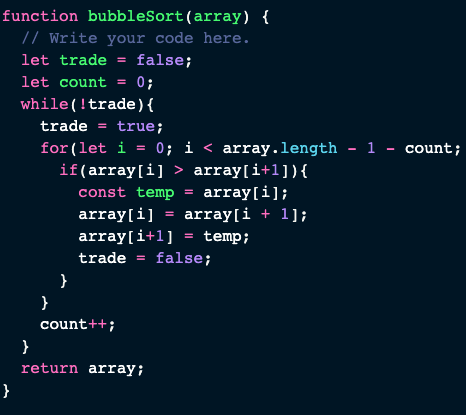
So lets look at the code:
Going through each line of the code the first thing we notice is that the function takes an array as a parameter. Duh!
The next thing we have declared in our function is a value labeled trade which is our sentinel value. We initialize this variable as false meaning that no trades (swaps) have occurred. Next we are going to declare a variable labeled count which is simply going to track how many times we have iterated through the array. This is especially important and it took me awhile to understand that we will use this to decrease the length of the array as we iterate through it again. Why do we do this...I will explain this shortly.
Now the for the actual iteration. The iteration through the array will be nested in a while loop. While loops run until the parameter set within their parenthesis is no longer true.
Inside the while loop our condition is our sentinel value. We are stating that while trade is false or when no values have been traded, we can continue our while loop. Nesting a for loop inside a while loop will give us a time complexity of O(n2). We have a space complexity of O(1) though as we are not requiring any more space to sort.
Now it might seem weird to immediately reassign the trade value but the reason we do this is that in the case we iterate and we make no swaps, the true value will allow us to escape our while loop.
Now we iterate through our array, declaring i as 0 to start at the index of the array, the stopping condition is if we reach 1 less than the length of the array but wait... minus the count? I mentioned this earlier and the reason we do this is that if we are sorting and taking the larger values to the end then we can expect that we don't need to iterate through the full length of the array each time as we would end up iterating over the large values at the end which are already sorted. Again, this took me a second or twenty to understand. Finally, i++ because simply we are going through the indexes of the array one at a time.
Our conditional check! If the current value is greater than the next value it is time to make a trade! Create a variable and assign it the value of the current value. Why? We do this because we are about to lose access to that value so we must store it. Alright, reassign then current value to be next value in the array. Now, assign the next value in the array to be the current we declared just moments ago. We assign trade to the value of false to continue to stay in the scope of our while loop. Now we can continue to iterate and swap where necessary. When we finish one iteration of our array we increment the count by one which will allow us to reduce the length of the array we need to iterate through.
If and when we iterate through the array and no values have been traded we will break out of our while loop. That was quite the journey but don't forget to return the array to complete this algorithm!








Top comments (0)