...and I am neck deep in the algebraic territory realizing monadic operations. It's a humid night, like I am still there, early morning, right before the dawn when its still so dark, hopelessly dark before the day breaks, and this is the day before the darkest moon in the month. My engines of expressions, thinking transforming information on pure functions, then results called "Algebra-Driven-Design" reading sample from a book by sum type Sandy Maguire. I have heard many times the goddess speak about algebraic reasoning, and was always fascinated by the idea of understanding, reasoning, sharpening the intellect, the mind stuff, the Buddhi by looking at equivalences, and it felt like a cool type of knowledge, something worth explore, a way to move the mind, an inclusive and intuitive movement. This approach seems to me in opposition to the one where we design, merely transfer biased operational solutions, assign guilt, gates and locks. But instead of commenting imperatively how we fail, I turn our passwords and keys into the samsaric realm, and they suddenly disappear, we begin to think equivalence, equality, and also side effect.
So I kept basically asking myself what is a monad, how is it built, and then it dawned on me, that monad is like encoding states of matter, like a purely geometric abstract space, a context holder, a certain type of a context holder within a constellation of a variety monadic operations within a monadic class that can operate on any program, its essence being so simple and profound. It does not exist in itself, it is no special thing, it kind of describes a thought,the space of reasoning, and how our reasoning is transferred between functions, transactions between pure functions, as a function it defines the space of side effects, separating the logic, without prejudice, realizing common patterns in side effects too, how they too have algebraic nature, realize everything and hold equality among programs too.
Monads in space:
So these are algebraically defined operations, equivalences. Wait, just look at the idea of passing a result from a function to another function. It is like a close circuit, like the falling bricks of dominoes, it begins at one point, the head domino, and then the rest, the tail just falls one after another. This is how I understand the concept of a list, actually the concept of recursively computing the remaining members of some List,
A List, a singly linked list, which is a data structure is defined by a almost like a self similar operation, while the monad has an extra type variable a which binds the external variable into the result of the next function. At least something like that.
I was not aware until now that the right side of this equation, this Haskell expression is itself made out of two sub-expressions and that the right expression is actually split into two sub-expression by the Div, the divide, (/) function. It also seems like a smart learning aid because the action of dividing any number makes two equal numbers, so is in this case also the so called size of both expressions similar or not?
Mona is a female, and sometimes male, given name and a surname of multiple origins.
but what about the I/O Monad? I never really inquired into the I/O itself, how it works, my attention mostly observing the monad next to it, I simply just accepted that I/O means input/output and continued to scan the monad creature.
But there was more to it, I wondered about words we held in our minds, in our awareness, in this attention span, which was actually focused at the monad words while the real actual monadic word was just there next to it, even written in capital letters, I/O.
So this looks super interesting:
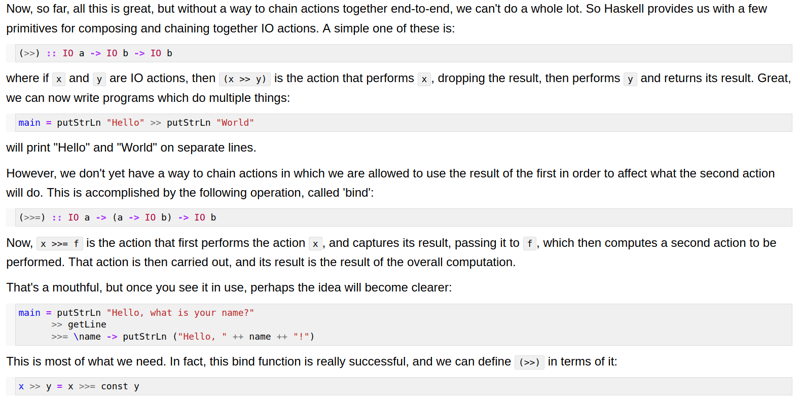
(>>=) :: IO a -> (a -> IO b) -> IO b
Woah, so (>>=) is some type of a symbol, a key that unlocks the doors of monadic operations, once opened a place is not gained but an understanding when and where ever you attention is, so (>>=) has a type, it is a typed symbol, with a meaning attached, and so like heavy rain falling on our rooftops, the sound of pressing keyboards penetrates everywhere, a type of an IO operation, that we just call a, like my name, like your name, like a name, or a word, or a string, Alice, a string of characters like Al, like AI, or just any character a. An event designated with IO and given a unique identifier a open to be anything
still, the haskell wiki says:
Now,
x >>= fis the action that first performs the actionx, and captures its result, passing it tof, which then computes a second action to be performed. That action is then carried out, and its result is the result of the overall computation.
But now I wonder what is the big deal with monads anyway? Why are they so hard to realize, is it just because they pass on changed value, the state within the system, chained geometric like processes, so similar objects could be actually anywhere, and scaling becoming easier, suddenly so natural and pure? The whole monadic operation embraces side effects as pure citizens and seems much more sensitive to time, its temporal flow..
While programs may describe impure effects and actions outside Haskell, they can still be combined and processed ("assembled") purely, inside Haskell, creating a pure Haskell value - a computation action description that describes an impure calculation. That is how Monads in Haskell help keep the pure and the impure apart.



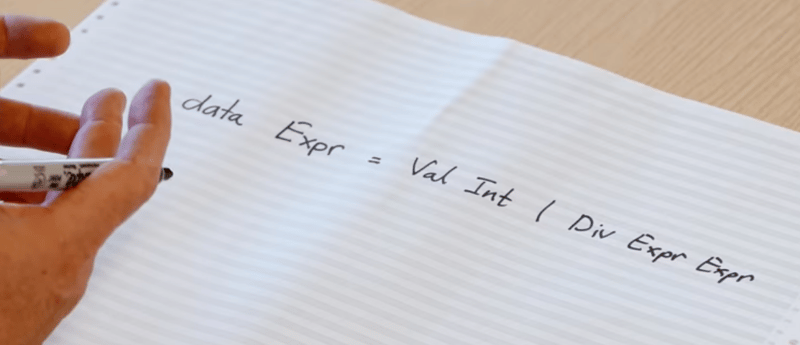







Top comments (0)