RPN expressions in Clojure, playing with macros.

TL;DR:

; Let's Calculate sqrt((((2*3)/a)*18+t)/X)

; That is annoying
(sqrt (/ (+ (* (/ (* 2 3) a) 18) t) X))

; That looks better (if you know how to look at it)
(rpn 2 3 * a / 18 * t + X / sqrt)

;CHANGE MY MIND

Hi everyone. This post is about writing arithmetic expressions in Clojure. Some people might find the parens a bit annoying or confusing when they are introduced to Clojure or LISP for the first time. However it's a matter of time to get used to parens plus if you follow a good coding style.

Michael Burge

@themichaelburge

f(5,6) - "The ideal syntax for practical programmers"
f 5 6 - "Bizarre; only academics would use"
(f 5 6) - "Too many parentheses"
5.f(6) - "Preferred for your next web app"

00:53 AM - 04 Nov 2018

893 2305

Although you can get very used to the syntax, it can be a real pain when you need to type an arithmetic expression like:

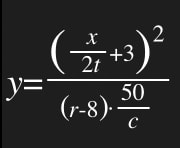
And to be honest, it doesn't matter what language you are using, you will use lots of parens, but Clojure's prefix notation + parens makes it even more confusing.

Since I was at high-school I used to have an HP scientific calculator for my maths and physics lectures. HP calculators are a bit special as they are setup by default with RPN notation, (demo).

What is RPN notation?

RPN stands for Reverse Polish Notation, and it's a completely different way of executing operations as opposed to infix notation.

RPN relies on a stack, where you push operands and whenever you want to apply an operation to the top elements of the stack. That will depend on the arity of the operation (+ arity is 2, whereas sqrt arity is 1). The way it will work is: it will pop the operands from the top of the stack, then it will execute the operation and the result will be pushed back to the top of the stack.

In UNIX systems you usually can find a RPN calculator in /usr/bin/dc.

Example:

Infix notation: (1 + 5) * 13 + 8 = 86
RPN: 1 5 + 13 * 8 +

STACK[]     :push 1
STACK[1]    :push 5
STACK[1 5]  :pop 5, pop 1, apply + to 1 and 5 (1+5), then push 6 
STACK[6]    :push 13
STACK[6 13] :pop 13, pop 6, apply * to 6 and 13, then push 78
STACK[78]   :push 8
STACK[78 8] :pop 8, pop 78, apply + to 78 and 8 (78+8), push 86 
STACK[86]   

Infix: ((1 + 5) * (2 / (1 - 7) + 5)) / 2 = 14
RPN: 1 5 + 2 1 7 - / 5 + * 2 /

STACK[]         :push 1    
STACK[1]        :push 5
STACK[1 5]      :pop 5, pop 1, apply + to 1 and 5, push 6
STACK[6]        :push 2
STACK[6 2]      :push 1
STACK[6 2 1]    :push 7
STACK[6 2 1 7]  :pop 7, pop 1, apply - to 1 and 7, push -6
STACK[6 2 -6]   :pop -6 pop 2 apply / to 2 and -6, push -2/6
STACK[6 -2/6]   :push 5
STACK[6 -2/6 5] :pop 5, pop -2/6, apply + to -2/6 and 5, push 28/6
STACK[6 28/6]   :pop 28/6, pop 6, apply * to 6 and 28/6, push 28
STACK[28]       :push 2
STACK[28 2]     :pop 2 pop 28 apply / to 28 and 2, push 14
STACK[14]       

That might look a bit over complicated, but trust me, when you get used to a RPN calculator you almost forget how to use traditional calculators (eg: classic CASIO). It's so much faster and easier to write big equations. It is true that usually you have extra tools to work with the stack, like dropping the top value or swapping top 2 positions, etc.

What I wanted to do in this post is writing a Clojure macro that allows you to write RPN expressions, so that it reshapes from RPN to standard prefix notation.

Example:

; (1 + 5) * 13 + 8
(rpn 1 5 + 13 * 8 +)
=> 86
(macroexpand '(rpn 1 5 + 13 * 8 +))
=> (+ (* (+ 1 5) 13) 8)

Now the big question. Is RPN better than standard Clojure prefix notation?. I think this is very subjective, it is true that you don't use brackets with RPN, but when the formula gets big it is hard to keep a large stack in your brain if you are reading the code. I have to say though that writing a formula is extremely easy to me, going back and trying to read it a week later is a different story.

This macro might not be very useful but has allowed me learn interesting concepts about writing macros.

Here you can find the macro, below you will find a REPL where you can play with it if you feel like.

(defmacro rpn [& args]
  (loop [[f & rst] args
         acc (list)]
    (cond
      (and (symbol? f) (ifn? @(resolve f)))
      (if (= 1 (count (:arglists (meta (resolve f)))))
        (recur rst  (cons (list f (first acc)) (drop 1 acc)))
        (recur rst  (cons (list f (second acc) (first acc)) (drop 2 acc))))

      (nil? f)
      (first acc)

      :else
      (recur rst (cons f acc)))))