Hello👋👋.Before we embark on this amazing article be sure to check out my last wonderful 🙂article on Data Structures and algorithms 101.
In this article, we will learn everything that we need to know about Big O notation and how you can use it to improve your ability to create efficient algorithms.
Big O notation is used to classify algorithms based on how fast they grow or decline. It is used to analyze the efficiency of an algorithm as its input approaches infinity.
For Example:
Let's say we have a dentist and she takes 30 minutes to attend to one patient. As her line of patients increases, the time that it takes to treat all of the patients will scale linearly with the number of patients waiting in the line.

This gives us a general understanding of how long our dentist would take to attend to any number of patients since she uses a constant amount of time, which is 30 minutes to treat each patient. With this in mind, we can categorize his efficiency as linear or as we say in big O terms big O of n (Big O(n)), where n is equal to the number of patients, the time that it takes for her to finish her work scales linearly or proportionally with the number of patients.
We can use the same technique to determine the general idea of how a function's time efficiency scales by categorizing a given function's efficiency in the same way as the dentist's efficiency. Let's create an easily comprehensible function that scales similarly to the dentist.
1. Finding the sum of numbers in a given array.
given_array = [1,4,3,2,...,10]
def find_sum(given_array):
total = 0
for each i in given_array:
total+=i
return total
One may ask how does the runtime of a function grow?
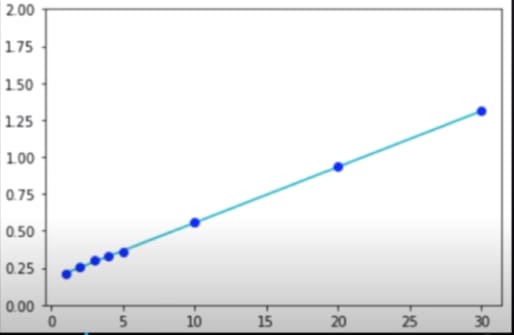
we run our functions to generate a bunch of arrays with various sizes as our inputs. These were:[5,7,9,7,8],[4,9,8,6,3],[1,9,7,1,10,7,6,7,9,4],[6,9,7,5,6,1,5,6,6,7]
Using these randomly generated arrays as input we run our function many times to find the average time it takes to run our function in each of n where n is the number of elements in a given array.
Note:
The X-axis represents the number of elements and the Y-axis represents the time in microsecond it takes to run a function.
From the graph, this is known as linear time complexity represented as O(n). Time complexity is a way of showing how the runtime of a function increases as the size of the input increases.
Other time complexities include:
1.Constant time: This is where the time to run a function does not increase with increase as the input increases. It is represented as O(1).
Example:
given_array=[1,4,3,2,...,10]
def stupid_function(given_array):
total = 0:
return total
When we run this function with various sizes of array inputs the result is as shown below.
Our constant c = 0.115 and it's the fastest-growing time.
2. Quadratic time: This is where the time to run function increases the way a quadratic function increases. It is represented as O(n^2).
Example:
array_2d = [[1,4,3], [[1,4,3,1],
[3,1,9], [3,1,9,4],
[0,5,2]]. [0,5,2,6],
[4,5,7,8]].
1. def find_sun_2d(array_2d):
2. total = 0
3. for each row in array_2d:
4. for each i in row:
5. total += i
6. return total
-Lines 2,5 and 6 take the same amount of time to run and thus have a constant time. In addition, we have 2 double for loops in our example which we assume do exactly the same thing. This would give us
T = O(1) + n^2 * O + O(1)
=O(n^2).
Thank you for Having time for my Article.🤗🥰️🎉
Thank you for taking your time to read 🤗🥳Happy learning😇🌟.









Top comments (0)