Table Of Contents
* 🤓 INTRODUCTION
* 👉🏻 ABOUT MERGE SORT ALGORITHM
* 👨🏻‍🏫 EXPLANATION
* 👀 VISUAL EXAMPLE
* 🛠 IMPLEMENTATION
* 👩🏻‍💻 CODE
* 🤔 COMPLEXITY
* 🙏 THANK YOU

🤓 INTRODUCTION

Welcome, hackers! I hope you are all having a great weekend.🚀Before we start another work week tomorrow, let's learn something new. In this blog article, we are going to explain and implement the Merge Sort algorithm.

👉🏻 ABOUT MERGE SORT ALGORITHM

Merge sort algorithm is another divide-and-conquer algorithm based on the idea of breaking down a list into several sub-lists until each sublist consists of a single element and merging those sublists in a manner that results in a sorted list.

Let's take a generic array that starts at index p and going through index r. It will be convenient to have a notation for a subarray, array[p..r]; In terms of our notation, for an array of n elements, we can say that the original problem is to sort an array A[0..n-1];

👨🏻‍🏫 EXPLANATION

Here is how merge sort uses divide-and-conquer:

Divide - by finding the number q of the position midway between p and r. Do this step the same way we found the midpoint in binary search: add p and r, divide by 2, and round down.

Conquer - by recursively sorting the subarray in each of the two subproblems created by the divide step. That is, recursively sort the subarray array[p..q] and recursively sort the subarray array[q+1..r];

Combine - by merging the two sorted subarrays back into the single sorted subarray array[p..r];

👀 VISUAL EXAMPLE

Steps:

0: Array [14, 7, 3, 12, 9, 11, 6, 2] is unsorted
1: Find q (q = (p+r)/2) q=3 in our case
2: We divide into two subarrays [14, 7, 3, 12] - up to the index of q - And [9, 11, 6, 2]
3: Find q again in this case for each of the subarray
The first subarray q index is 1 and for the second q=5
4: We divide into the following subarrays:
[14, 7] and [3, 12] for the first subarray and [9, 11] and
[6,2] for the second subarray.
...Repeating these steps until we have only single values as an array member. We have to make two recursive calls in the conquer step.

🛠 IMPLEMENTATION

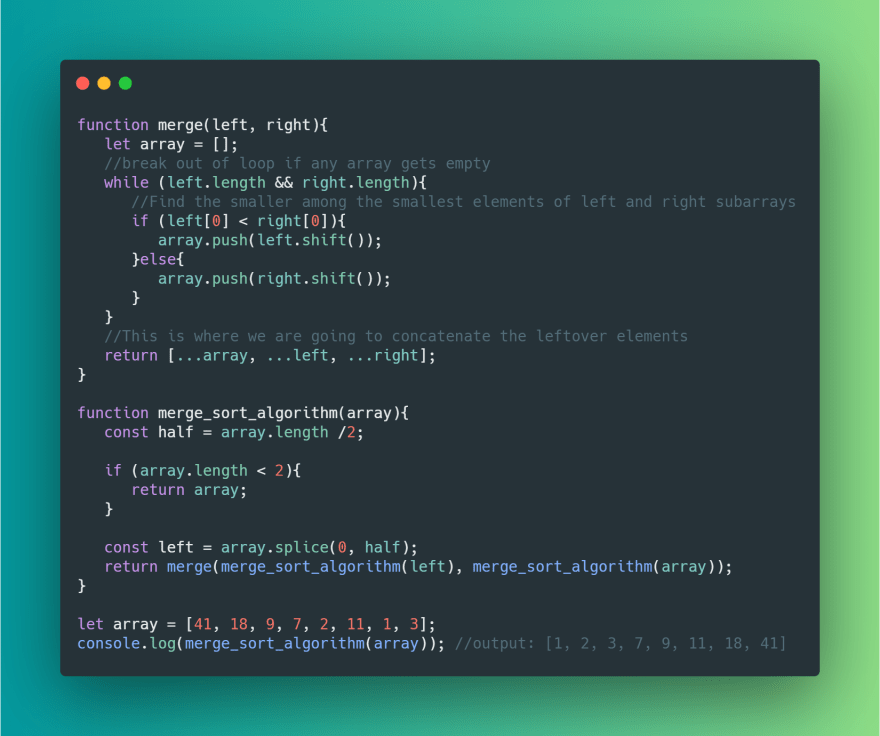
👨🏻‍💻 CODE

Play with the code!

🤔 COMPLEXITY

The complexity of the Merge sort algorithm is in the very best case Big O of nlog₂n, in the worst case, the merge sort is staying consistent with the complexity of Big O of nlog₂n.
The bad thing about the Merge sort algorithm is that requires an extra memory space the same size as the vector that is being sorted.

🙏 THANK YOU FOR READING!

References:
School notes...
School books...
Khan Academy

Please leave a comment, tell me about you, about your work, comment your thoughts, connect with me!

☕ SUPPORT ME AND KEEP ME FOCUSED!

Have a nice time hacking! 😊