Problem statement
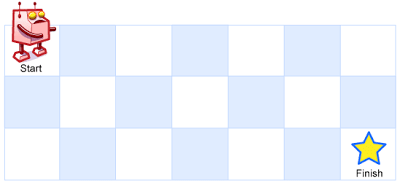
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Problem statement taken from: https://leetcode.com/problems/unique-paths
Example 1:
Input: m = 3, n = 7
Output: 28
Example 2:
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
Example 3:
Input: m = 7, n = 3
Output: 28
Example 4:
Input: m = 3, n = 3
Output: 6
Constraints:
- 1 <= m, n <= 100
- It's guaranteed that the answer will be less than or equal to 2 * 10^9
Explanation
Brute force approach
As per the problem statement the robot can move either down or right. We can use recursion to find the count. Let numberOfPaths(m, n) represent the counts of path to reach row number m and column number n in the grid. numberOfPaths(m, n) in C++ can be recursively written as following.
int numberOfPaths(int m, int n){
if (m == 1 || n == 1)
return 1;
return numberOfPaths(m - 1, n) + numberOfPaths(m, n - 1);
}
The time complexity of the above solution is exponential.
There are many overlapping sub-problems and hence we can use
dynamic programming approach to avoid re-computing
overlapping sub-problems.
Dynamic programming approach
We can avoid re-computing the overlapping sub-problems by constructing a temporary 2D array count[][] in bottom up manner using the above recursive approach.
int numberOfPaths(int m, int n){
// create a 2D array to store results of sub-problems
int count[m][n];
// count of paths to reach any cell in first column is 1
for (int i = 0; i < m; i++)
count[i][0] = 1;
// count of paths to reach any cell in first row is 1
for (int j = 0; j < n; j++)
count[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++)
count[i][j] = count[i - 1][j] + count[i][j - 1];
}
return count[m - 1][n - 1];
}
The time complexity of the above program is O(mn). The space complexity is O(mn). We can reduce the space more by O(n) where n is column size.
int numberOfPaths(int m, int n){
int count[n] = { 1 };
count[0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 1; j < n; j++) {
count[j] += count[j - 1];
}
}
return count[n - 1];
}
Combinatorics approach
We have to calculate m+n-2 C n-1 here which will be (m+n-2)! / (n-1)! (m-1)!
Let's check the algorithm on how to compute the above formula:
- set paths = 1
- loop for i = n; i < m + n - 1; i++
- set paths = paths * i
- update paths = paths / (i - n + 1)
- return paths
C++ solution
class Solution {
public:
int uniquePaths(int m, int n) {
long int paths = 1;
for(int i = n; i < m + n - 1; i++){
paths *= i;
paths /= (i - n + 1);
}
return int(paths);
}
};
Golang solution
func uniquePaths(m int, n int) int {
paths := 1
for i := n; i < m + n - 1; i++{
paths *= i
paths /= (i - n + 1)
}
return paths
}
Javascript solution
var uniquePaths = function(m, n) {
let paths = 1;
for(let i = n; i < m + n - 1; i++){
paths *= i;
paths /= (i - n + 1);
}
return paths;
};
Let's dry-run our algorithm to see how the solution works.
Input: m = 3, n = 7
Step 1: set paths = 1
Step 2: loop for i = n; i < m + n - 1
i = 7
7 < 7 + 3 - 1
7 < 9
7 < 9
true
paths = paths * i
paths = 1 * 7
= 7
paths = paths / (i - n + 1)
= 7 / (7 - 7 + 1)
= 7 / 1
= 7
i++
i = 8
Step 3: loop for i < m + n - 1
8 < 8 + 3 - 1
8 < 9
8 < 9
true
paths = paths * i
paths = 7 * 8
= 56
paths = paths / (i - n + 1)
= 56 / (8 - 7 + 1)
= 56 / 2
= 28
i++
i = 9
Step 4: loop for i < m + n - 1
9 < 8 + 3 - 1
9 < 9
false
Step 5: return paths
So we return answer as 28.






Top comments (0)