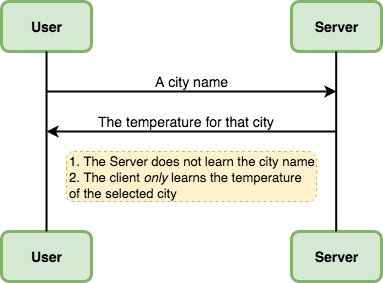
Consider a weather app that you have on your phone. For most users, this app records the current GPS location, sends it to a server and receives and displays the temperature of the user's location. This means that if the server chooses to, it can create a profile of the user location history and track their movement which is a breach of privacy for most users. Therefore, a privacy-aware user might want to obtain weather information without sharing their location. Let's call this User Security Property.
Designing an application that satisfies this security property is very easy. In fixed intervals, the server sends all the weather information it has for all the cities and regions from all over the world to the user's device and the user does a local lookup to find the weather information that is interesting to them. As you can see, with this approach the server has no way of knowing the user's location. Unfortunately, this approach has two main problems.
- The amount of data that is sent to the user's device is too large.
- More importantly, the user learns all the weather information which is the backbone of the business that the server is running.
Therefore, we are interested in a solution that is fast and efficient enough to be used in practice (this is a very subjective criterion and depends on the use case). We are also interested in a solution that protects the privacy of the server and only sends the temperature of the city that the user has asked for. Let's call this Server Security Property.
To sum up, we have two parties a server and a user. The server has a list of private temperature data and the user has a private input which indicates the city that the user is interested in. We would like to offer this functionality such that the User Security Property and Server Security Property are satisfied and that the solution is more efficient than sending all the server data to the user.
Oblivious Transfer can help with achieving this goal. To describe Oblivious Transfer (OT), we first consider a simple case where the server only holds the weather information about two cites and the user chooses one of those cities. This case is called 1-out-of-2 OT. In what follows, I'll describe the theory and some code snippets and then describe how to extend it to more than two cities.
Theory
One of the simplest OTs (specially if you know Diffie-Hellman key exchange protocol) is proposed by Chou, Orlandi 2015. The overall protocol is shown in the figure below. But it is not immediately clear what is happening there and what are a, b, g, Hash,Encrypt, and Decrypt.
What is g?
g is the generator of a "simple group" of prime order p. For example, consider the group of Z11 which is a group of prime order 11 and therefore has 11-1 members {1,2,...,10}. This is a cyclic group if you consider g=2 since you can create all the members of the group by starting from 2 and keep multiplying it by 2. In other words {21,22,23, ..., 210} module 10 produces the same set as {1,2,...,10}.
To see it for yourself, run the following program.
def generate_group(g, p):
# Using list to show that there are not duplications
members = list()
for i in xrange(1,p):
members.append(g**i % p)
return sorted(members)
generate_group(2, 11)
# => prints [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
What are a and b?
a and b are two integers that are selected at random from the Z11. Note that both of these values appear as the exponents of g and therefore ga and gb result in a member of the cyclic group.
What are Hash and Encrypt/Decrypt?
The proper definition of the Hash and Encrypt functions can be found in the paper, but for our purposes assume Hash is SHA1 and Encrypt/Decrypt is a symmetric key encryption scheme such as AES.
Does the Protocol Work?
To show that this protocol is doing what it claims, let's follow it with an example. In this example, we use the same group Z11 and with g=2 as its generator. Also, assume that a=4 is chosen uniformly at random and similarly, b=7 is chosen uniformly at random. The following code computes the steps required for the user to obtain k and for the server to obtain k0 and k1. You will notice that if the user sets c=0, then k will be the same as k0 and if the user sets c=1, then k will be equal to k1. Therefore, the user can either decrypt e0 or e1 based on their choice, but they CANNOT decrypt both.
# multiplies x to the inverse of y
def div(x, y, p):
xp = x % p
yip = pow(y, p-2, p)
return (xp * yip) % p
def examine_case_c_0(g, a, b, p):
A=pow(g, a, p)
B=pow(g, b, p)
k=pow(A, b, p)
k0=pow(B, a, p)
k1=pow(div(B, A, p), a, p)
print(k, k0, k1, k == k0)
def examine_case_c_1(g, a, b, p):
A=pow(g, a, p)
B=(A * pow(g, b, p)) % p
k=pow(A, b, p)
k0=pow(B, a, p)
k1=pow(div(B, A, p), a, p)
print(k, k0, k1, k == k1)
examine_case_c_0(2, 4, 7, 11)
# => (3, 3, 4, True)
examine_case_c_1(2, 4, 7, 11)
# => (3, 5, 3, True)
So far, we have demonstrated that the protocol is correct. To actually prove its correctness, you can just write down the formulas and go through the math. Next, we will talk about the security of the protocol and try to argue that it satisfies both of the security requirements.
Is the Protocol Secure?
To examine the security of the protocol, imagine that you are the attacker and see what you can do! For example, let's assume that you are the server and your goal is to find out the user's choice of the city. Looking at the protocol, you'll notice that as the server you are getting only one message. Depending on the user choice, you either get B=gb or B=Agb. Therefore, if you can somehow identify which message you got, you have succeeded in your attack. Let's consider a couple of different ways that you can perform your attack. In other words, we want to find ways that we can violate User Security Properties. Our attacks will involve finding or guessing b. Note that both the user and the server know g. Therefore, if we can find/guess b, then we can compute gb and compare the result with B. If they are the same, we know that the user has chosen city0. We (the server) can perform this attack in two ways.
- By finding a flaw in the way
bis generated: if the user choosesbrandomly and implement the random gen code properly, then the user is safe against this type of attack. Therefore, we define
User Security Requirement 1: Use secure random to choose "b" and do not reuse "b".
- By trying all possible values of
b(i.e., a brute-force attack). If our cyclic group is big enough, then this attack would be impractical. Therefore, we define
User Security Requirement 2: Choose a large enough cyclic group such that brute-forcing "b" is impractical for the duration that "b" is valid..
We can also make the same kind of arguments about the requirements for satisfying Server Security Property which I leave for you to explore and think about. In particular, I encourage you to read about the hardness property of the discrete logarithm problem and how it relates to Diffie-Hellman problem.
From the above arguments, we have identified that to satisfy User Security Property, the protocol implementation must be configured such that it satisfies the following requirements.
- The implementation must generate
busing secure random every time. - The implementation must use a cyclic group with a very large size to prohibit the brute-force attack.
Now, are these arguments enough to prove security and more importantly, is the approach that we have taken so far a good approach for proving security? The above arguments are informal and are not accurate. For example, we have not defined the "large enough" size for the cyclic group, nor have we defined the "hardness" property of the discrete logarithm in the cyclic group. Moreover, we have described the random number generator as "secure" without specifying what it means. Nevertheless, this approach towards proving security is a correct approach and it is how real proofs look like. Namely, going over each message that a party receives and proving that the message leaks no information about the private input of the parties. I will write about the proof model in a separate post, in the meantime, you can read about them in a concise tutorial by Yehuda Lindell, or get a more in-depth knowledge by reading the wonderful books by Oded Goldreich, Foundations of Cryptography, Vol I and II.
Back to the Application
We started with the goal of creating a weather reporting service that preserves the privacy of the user and the server and introduced Oblivious Transfer (OT) as a potential solution. We then showed how an OT protocol can be designed for the case where the server has only two city temperatures and the user chooses one of them (1-out-of-2 OT). Now, we want to extend this to a 1-out-of-n OT for some large n. A naive approach is to create a network of 1-out-of-2 OTs, where each pair of initial temperatures are fed to an OT and then create another layer of OTs such the output of each pair of OTs from the first layer is fed to an OT in the second layer and so on. This forms a binary tree and requires approximately n OTs. There are much faster solutions which can achieve this with a constant number of 1-out-2 OTs.
At last, the following code shows an implementation of this application using libOTe. You can find a docker file which sets up and runs this program on my repo.
Final Remarks
Similar to the previous post, just implementing a secure protocol is not enough and there are much more things that one need to take into account. For example, on preserving the privacy of the user, note that the user's location can be found (or at least estimated) through the source IP or network delays. Moreover, based on the frequency of the weather checks and the requests to the server, the server can guess whether the user is traveling on the road or not. Nevertheless, using a secure protocol is far better than a non-secure one.







Top comments (3)
You should use "his" not "their" when talking about a user.
To encourage inclusivity, "their" is the preferred pronoun when talking about a generic user (or at least preferred over "his" or "hers").
It may be the current politics in Silicon Valley, but it is bad grammar, and makes it difficult to read.