If you missed the previous article in this series (Divide and Conquer), you'll want to read it first so you understand what we're going to be discussing here.
The Sobel operator approximates the gradient magnitude and direction of an image at a specific pixel, but it can theoretically be applied to any discrete function of two variables. For those who don't remember or haven't studied multivariable calculus, let's discuss what that means. Otherwise, if you're familiar with calculus, feel free to skip past the next few sections of this article.
Derivatives
Single-variable mathematical functions take a single, numeric input variable and produce a single, numeric output. Simple, right? Here's an example:
If we were to write that in JavaScript:
function f(x) {
return 3 * x;
}
console.log(f(1)) // 3
console.log(f(2)) // 6
// You get the idea...
If we plot the output on a vertical axis and the input on the horizontal axis (i.e. y = f(x)), we get this nice line:
You already know this, of course. Things get a bit more interesting when we calculate the slope of this line, which is a numerical representation of the "steepness" of the line and is computed by calculating "rise over run." Steeper functions have greater slopes. In this case, the function rises by 3 every time it runs by 1 (the y-value goes up 3 each time x goes up 1). Therefore, the slope is 3 / 1, or 3. We could also have seen that it rises up by 6 every time it runs by 1, and we would find the slope to be 6 / 2, which also evaluates to 3.
More specifically, the slope represents the rate of change of a function, or how much the function's output changes for a change in the input of 1.
What's the slope of a more complicated function, say
? If we plot it, we see that the function gets more steep the further you go from x = 0, so the slope can't just be represented by a single number.
As it turns out, this function doesn't really have a slope. We can only calculate the slopes of the tangent lines at each value of x. The tangent line is a linear approximation of the original function that is identical to it near some point. Here's a plot of the function with a tangent line at x = 1:
The blue line seems to become the same as the red curve near x = 1, since (1, 1) is the point of tangency. As I mentioned above, we can calculate the slope of the tangent line at any point on the red curve. For this function, it turns out that the slope of the tangent line is equal to 2x at any x-coordinate. We call this the derivative of the function; the derivative is often denoted with an apostrophe we call "prime." Therefore:
We can say that "f-prime of x is 3, and g-prime of x is 2x" because for f(x), the tangent line is actually the same as the function itself (a property of all linear functions) and so the derivative is just the slope, whereas for g(x) we have to do some more work to find the slope of the tangent line. We'll get to why we care about the derivative in a second.
The derivative of a function is the instantaneous rate of change of that function. I don't want to make this article only on math, so I've skipped over a lot of details that you should really learn if you've never studied calculus (including how you actually calculate the derivative for an arbitrary function!) I highly recommend Khan Academy's Calculus 1 course, or this excellent video if you're in a rush.
Multivariable functions
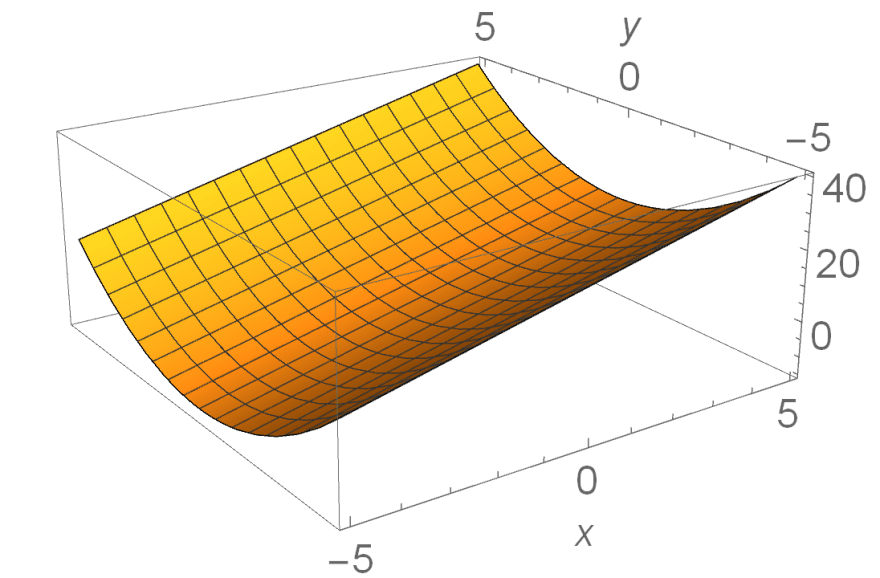
Multivariable functions are often confusing to math students, but as a programmer you use them all the time! They're just functions that have more than one input variable. Here's an example:
In JavaScript, that's just:
function f(x, y) {
return 3 * x + y * y;
}
It's a bit harder to visualize mentally since we can't graph this on a 2-D plane anymore; we'd need a 3-D surface to show what this looks like. The function has both an x-axis and a y-axis for input, and now uses a z-axis for output. In the following image, the z-axis is vertical and the x- and y-axes are horizontal.
It doesn't really make sense to take a derivative of this function: it's a 3-D surface, not a curve, so there's an infinite number of tangent lines you can take at each point (x, y, f(x, y)) in every direction.
However, we can take the derivative if we specify which direction our tangent line is pointing on the horizontal plane. For example, we can calculate the slope of the tangent line in the positive-x direction. This is called the partial derivative with respect to x. We can do this for any arbitrary direction, but for many cases we only care about the partials with respect to the input variables (in this case, x and y). For this function:
That means that the partial derivative with respect to x is 3, and the partial with respect to y is 2y. Taking partial derivatives is very easy if you know how to calculate derivatives: consider all other variables to be constants when you differentiate with respect to one. For example, when taking the partial with respect to x, we simply assume y is a constant value and therefore can disregard the y^2 term. (You can't just assume the values are zero, though; the partial with respect to x of xy is still y.)
There's a useful value for continuous multivariable functions called the gradient vector. If you're familiar with vectors, the gradient for a function of two variables (x and y) is defined as:
In many cases, we really only care about the gradient direction and magnitude (which uniquely define the vector anyway). For any specific x and y, the gradient direction is the direction of "steepest ascent," i.e. the direction in the XY plane in which the output of the function is increasing the most, while the gradient magnitude is the value of the derivative in the gradient direction (in other words, the slope of the steepest tangent line in any direction at (x, y, f(x, y))). Here's how you compute these values (the bars represent magnitude, and theta is the angle):
If you've never done multivariable calculus before, this all may seem confusing, but it should start to feel quite intuitive over time if you truly understand preliminary calculus! Again, Khan Academy is your friend.
Where's the Computer Vision?
You may be wondering how all this theoretical math actually applies to document scanning. First, you need to rethink your idea of what an image is.
You probably already know that images are merely massive grids of pixels, where each pixel has a red, green, and blue, and potentially an alpha (opacity) value. Each of these values typically ranges from 0 to 255 (i.e. one byte represents each color/channel). By varying the values of each channel, you can create virtually any color from a single pixel, and together these colors make an image that can be displayed on screen.
Let's simplify things a bit by considering a grayscale image instead. Now, there's only one channel per pixel, which represents intensity. Let's also stop thinking of channels in terms of bytes and instead as merely real numbers (a floating-point value rather than an integer). So we have a grid of real numbers representing the brightness of the image at each pixel, or effectively at each point, in the grid. Now try to imagine that this image is actually just a function of x and y (which represent the coordinates of each pixel) that has an output of the image intensity. For example, if there's a brightness of 0.5 at the pixel at the thirtieth column from the left and the eight row from the bottom, we could say that:
One question that might be running through your mind is "how exactly can an image be a function? We don't have intensity between pixel values. What's f(30.27, 8.13)?"
Although most functions you'll run across in standard math courses have a domain of all real numbers (that is, they are defined at every possible finite point), some functions are not defined everywhere. For example, f(x) = 1 / x is not defined at zero because 1 / 0 does not exist. The image is defined at only the specific integer coordinates where the image has a pixel, but it still qualifies as a function. So, in short f(30.27, 8.13) does not exist, nor does f(12, 1.5) or f(-1, 100).
Now, let's say we want to find the gradient of this image. Just like all other functions of more than one variable, it should be possible to take the gradient, right? Unfortunately, we have a problem: it's impossible to take the derivative of a function at a point where it is not continuous, so we can't calculate the partial derivatives and can't find the gradient.
Therefore, the best we can do is calculate an approximation of the gradient of the image. Over the years multiple heuristic and theoretical methods for estimating the gradient have been discovered, but one of the earliest techniques, the Sobel operator, has remained popular because it is relatively inexpensive while remaining accurate enough for most applications.
The Sobel operator specifies two convolution kernels that can be used to compute the partial derivatives with respect to x and y at each pixel. Popular variants of the Sobel kernels are as follows:
For each of the above matrices, the convolution finds every 3x3 pixel region in the image and multiplies each intensity by the corresponding value in the matrix, then sums the results. The computed partial derivatives apply to the center pixel (which would be the second row, second column in each matrix). Using the partial derivatives, it's trivial to calculate the gradient magnitude and direction.
Here's an awesome video that explains convolutions in much better detail with some nice visualizations. You'll even learn how some neural networks work!
This algorithm was found to be effective after years of research and testing, so you don't need to understand why it works so well at approximating the gradient. However, you should be able to get a general intuition about what it does.
Consider the Sx matrix. If the intensities are about equal to the left and right of the center pixel, we can assume that not much change in the x-direction about the center pixel. As such, the weighted values cancel each other out since the filter is symmetric across the second column, and the calculated partial derivative is 0. However, in the following example the pixel values are very different:
Logically, since the values change greatly, the rate of change must be high, so the partial derivative with respect to x must be large as well. It is estimated to be:
Since the maximum possible magnitude of the derivative with this convolution is 16, a magnitude of 7 is relatively high.
It's very important to keep in mind that the gradients computed by the Sobel operator are only meaningful in relation to each other, since modifying the weights would change the maximum magnitude of the computed derivative. If your aim were to calculate the partial derivative for an actual mathematical function rather than an image, the Sobel operator would not only yield inaccurate results but would also be scaled incorrectly. A more appropriate technique to estimate the partial derivative with respect to x on samples of actual, mathematically expressible function would be applying the following convolution kernel:
This filter finds the slope of a linear approximation of the function using the two points one unit away from the center point in x, which is a theoretically more accurate estimation of the derivative.
To summarize: using some mathematical techniques, you can estimate the gradient vector for each point in an image even though discrete functions like images don't actually have derivatives.
Why do we care about the gradient of an image?
Let's go back to what the gradient actually represents. It describes the greatest rate of change you can find in any direction at some point in a function. For our image, the gradient encodes the greatest change in intensity that exists around a given pixel. If you think about it, what we visually consider to be the "edges" of things we see in an image are actually just pixel locations at which the intensity is change dramatically.
For example, at the edge of a piece of paper, the intensity changes from almost 1 (white) inside the paper to the intensity of the background across three pixels, causing a high gradient magnitude on edge pixels, whereas inside the paper any 3x3 region will have near-one values in all locations, yielding a very low gradient magnitude. Therefore, if we take the gradient magnitude of an image, we effectively emphasize the edges of all the objects in the image while suppressing areas with little change (i.e. the insides of those objects). A visual example should make this more clear. Original image:
Gradient magnitude:
Notice how the edges of the paper are almost white, and the outline of the text inside the page is gray, while the rest of the image is nearly black. This is the most critical step of edge detection and therefore is one of the key components of this document scanning app.
It's important to note that before actually doing the Sobel edge detection, we typically use a Gaussian blur to reduce the effects of image noise (which are often detected as edges due to the random spikes in intensity they cause). Additionally, we've downscaled the image substantially before even starting this process to reduce processing time.
However, we'll get to those steps in future articles, near the end of this series. Next, we'll discuss how we can use this gradient magnitude image to actually find mathematical representations of the edges in the image via the Hough transform.











Top comments (1)
Awesome article!